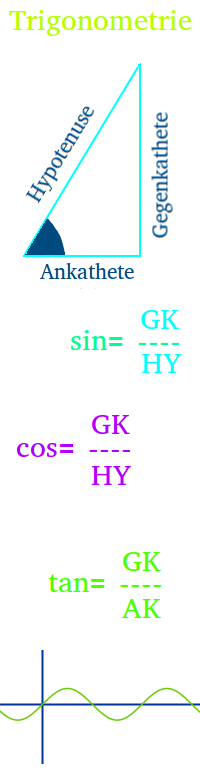Trigonometrie
Sin, cos, tan
© 2016
- 2025
Basiswissen|
Einführung|
Definitionen|
Sinus Cosinus Tangens|
Standardberechnungen|
Lehrsätze|
(Text)Aufgaben|
Wertelisten|
Sonstiges|
Funktionen|
Fußnoten
Basiswissen
Unter dem Überbegriff Trigonometrie werden verschiedene Verfahren zur Berechnung von Längen und Winkeln an Dreiecken zusammengefasst. Das zentrale Konzept ist der Tangens, Cosinus und Sinus.
Einführung
Wörtlich übersetzt meint Tri-gon-o-metrie: die Vermessung oder Berechnung von Dreiecken. Als Teilgebiet der Mathematik beschäftigt sich die Trigonometrie aber direkt nur mit der Berechnung von Längen und Winkeln an Dreiecken. Man kennt zum Beispiel die Längen aller drei Seiten in einem Dreieck. Jetzt will man damit die Größe der drei Innenwinkel berechnen. Das wäre eine typische Aufgabe aus der Trigonometrie. In einem engeren Sinn bezieht sich die Trigonometrie aber nicht auf alle möglichen Berechnungen mit Dreiecken, sondern auf die Berechnung fehlender Seitenlängen oder Innenwinkel wenn man wiederum Seiten und Innenwinkel gegeben hat (sinus, cosinus, tangens). Der gedankliche Ausgangspunkt fasst aller Rechenmethode ist so gut wie immer ein 👉 rechtwinkliges Dreieck
Definitionen
Sinus Cosinus Tangens
Standardberechnungen
Lehrsätze
(Text)Aufgaben
Wertelisten
Sonstiges
Funktionen
Fußnoten
- [1] Die Anfänge der Trigonometrie zur Landvermessung liegen im 17ten Jahrhundert. Vorher hatte man lange Strecken mit zum Beispiel Rädern und Ketten gememessen: "In 1525, the French mathematician Fernel measured the length of a degree of latitude between Paris and Amiens by the revolutions of the wheels of his carriage, the circumference of which he had deter-mined. In England, Norwood in 1635 measured the length of an arc between London and York with a chain. An important forward step in geodesy was the measurement of distance by triangulation, first by Tycho Brahe, in Denmark, and later, in 1615, by VVillebrord Snell, in Holland." In: Victor F. Lenten and Robert P. Multbauj: Development of Gravity Pendulums in the 19th Century. Contributions from The Museum of History and Technology: Paper 44. Bulletin - United States National Museum. Online: https://repository.si.edu/bitstream/handle/10088/21316/1/USNMB-240_44_1965_478.pdf