Basiswissen

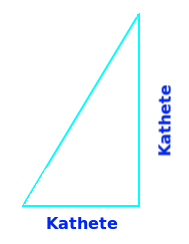
Jede der zwei kürzeren Seiten in einem rechtwinkligen Dreieck nennt man eine Kathete: eine Kathete gibt es nur in einem rechtwinkligen Dreieck. In einem ebenen, rechtwinkligen Dreieck gibt es immer ein längste Seite und zwei kürzere Seiten. Jede der zwei kürzeren Seiten nennt man eine Kathete. Mehr dazu unter Katheten ↗

Bildbeschreibung und Urheberrecht — Ein rechtwinkliges Dreieck hat immer zwei Seiten, die direkt am rechten Winkel, also am 90°-Winkel liegen. Diese zwei Seiten sind die Katheten. Es sind immer auch die zwei kürzesten Seiten im rechtwinkligen Dreieck.☛

Wie berechnet man die Länge einer Kathete?

Dazu gibt es verschiedene Verfahren:

Pythagoras, Tangens, Sinus, Cosinus etc.

Lies mehr unter Kathete berechnen ↗

Eine interessante Ausnahme

Oben wurde gesagt, dass die zwei kürzeren Seiten in einem rechtwinkligen Dreieck immer die Katheten sind. In diesem Satz ist die Annahme enthalten, dass jedes rechtwinklige Dreieck immer auch eine längere und zwei kürzere Seiten hat. Diese Annahme ist richtig, solange man rechtwinklige Dreiecke auf einer flachen Ebene, etwa einem Tisch zeichnet. Man wird dann immer feststellen, dass die Seite gegenüber dem rechten Winkel die längste Seite ist, also die Hypotenuse. Und die zwei Seiten direkt am rechten Winkel sind die beiden kürzeren Seiten die Katheten. Das stimmt aber nicht mehr, wenn man ein rechtwinkliges Dreieck auf einem Globus zeichnet.^[2] Dort kann ein Dreieck sogar zwei rechte Winkel enthalten und alle drei Seiten sind gleich lang.^[3] Damit macht auch die Unterscheidung von Katheten und einer Hypotenuse im Dreieck keinen Sinn mehr. Die Rechenregeln, die dann gelten, gehören in die sogenannte sphärische Geometrie ↗

Fußnoten

[1] Der "Brockhaus", ein Lexikon, definiert kurz: "Katheten, die beiden kürzeren Seiten eines rechtwinkligen Dreiecks." In: Brockhaus in Achtzehn Bänden. F. A. Brockhaus. Leipzig, Mannheim. 2002. ISBN für alle Achtzehn Bände gemeinsam: 3-7653-9320-7. Der Band 7. Seite 270.

[2] Zum sphärischen Dreieck, also einem Dreieck, das man auf der Oberfläche einer Kugel gezeichnet hat, heißt es. "A triangle drawn on a sphere is called a spherical triangle. Each side of a spherical triangle is required to be a geodesic; hat is, it is reuired to be intrinsically straight in the sense that a Flatlander on the sphere would perceive it as bending neither to the left nor to the right." In: Jeffrey R. Weeks: The Shape of Space. CRC Press. 2002. ISBN: 13-978-0-8247-0709-5. Dort im "Chapter 9. The Sphere". Seite 136.

[3] Ein rechtwinkliges Dreieck mit drei genau gleich langen Seiten kann man auf einem Globus konstruieren. Sie dazu den Artikel zum Galapagos-Dreieck ↗