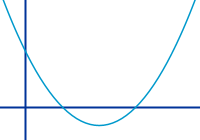
Quadratische Funktion

f(x)=ax²+bx+c

Basiswissen

Beispiele

• f(x) = 4x²-32x+60 mit a=4; b=-32 und c=60
  

• f(x) = 4x²-10x mit a=4; b=-10 und c=0
  

• f(x) = 4x²+50 mit a=4; b=0 und c=50
  

• f(x) = 4x² mit a=4; b= und c=0
  

• f(x) = x² mit a=1; b=0 und c=0
  

Ausführlich

• Auf der linken Seite vom Gleichzeichen steht das f(x).
  

• Das f(x) meint dasselbe wie y, beides ist erlaubt.
  

• Rechts vom Gleichzeichen stehen folgende Glieder:
  

• Ein x-Quadrat, eventuell mit einem Faktor davor.
  

• Beispiele: f(x) = x² (ohne Faktor) oder f(x) = 4x² (mit Faktor)
  

• Der Faktor vor dem x-Quadrat darf nicht Null sein.
  

• Der Faktor vor dem x-Quadrat darf aber negativ sein.
  

• Dann kommt ein Plus- oder Minuszeichen.
  

• Dann kommt ein Term mit x ohne Hochzahl.
  

• Beispiel: f(x) = 4x² + 9x
  

• Vor dem x darf ein beliebiger Faktor stehen.
  

• Dieser Faktor darf auch eine 0 sein.
  

• Erlaubt ist z. B.: f(x) = 7x² + 0x
  

• Dann kommt wieder ein Plus- oder Minuszeichen
  

• Am Ende kommt eine Zahl ohne x.
  

• Diese Zahl darf auch eine Null sein.
  

Beispiele

• f(x) = x²
  

• f(x) = 0,5x² - 8
  

• f(x) = 3x² + 4x - 5
  

Fachsprache

• Die Zahlen für a, b und c heißen => Koeffizienten
  

• Die Zahl vor dem x² heißt => Leitkoeffizient
  

• Die Zahl vo rdem x² heißt auch => Öffnungsparameter
  

• Der Term ax² heißt => quadratisches Glied
  

• Der Term bx heißt => lineares Glied
  

• Der Term c heißt => absolutes Glied
  

Klassifizierung

• Eine quadratische Funktion ist immer auch eine ganzrationale Funktion.
  

• Gibt es nur ein quadratisches Glied, heißt sie auch Polynomfunktion.
  

Graph

Formen

Synonyme

Übersichten

Besondere Punkte

Nullstellen

Umwandlungen

Aufstellen

Textaufgaben

Sonstiges