Definition

Jede Funktion, die sich umformen lässten in f(x) = a·b^T(x) heißt Exponentialfunktion. Das T(x) ist irgendein Term, bei dem eines oder mehrere x'se vorkommen. Bei einer Exponentialfunktion kommt immer ein x in einem Exponenten vor, daher auch der Name. Ist die Basis b der Potenz die Eulersche Zahl e, spricht man auch von einer e-Funktion. Das ist hier näher erklärt.

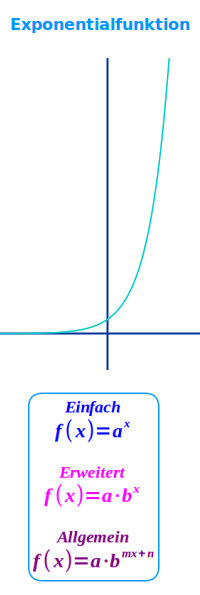
Bildbeschreibung und Urheberrecht — f(x) = 2^x mit dem typischen Graphen einer Exponentialfunktion: von links nach rechts erst ein flacher Anstieg, der dann aber schnell immer steiler wird.☛

Allgemeiner Bauplan einer Exponentialfunktion

f(x) = a·b^T(x)

Legende

a = Vorfaktor

b = die Basis: eine beliebige, konstante positive reelle Zahl.

^ = das Hochzeichen a^x ist dasselbe wie aˣ, sprich: a-hoch-x

T(x) = ein Term (Ausdruck) in dem eines odere mehre x's vorkommen

Beispiele für Exponentialfunktionen

f(x)=2^x als 👉 einfache Exponentialfunktion

f(x)=e^x als Sonderfall 👉 e-Funktion

f(x)=0,5·1,2^x als 👉 erweiterte Exponentialfunktion

f(x)=2^(4x-1) als 👉 allgemeine Exponentialfunktion

Siehe auch 👉 Exponentialfunktionen

Graph einer Exponentialfunktion

Heißt 👉 Exponentialkurve

Der Graph der Grundfunktion f(x)=e^x geht immer durch (0|1).

Der y-Achsenabschnitt ist also immer (0|1).

Der Graph hat nie eine 👉 Nullstelle

Der Graph hat nie einen 👉 Hochpunkt

Der Graph hat nie einne 👉 Tiefpunkt

Der Graph hat nie einen 👉 Wendepunkt

Der Graph ist überall 👉 linksgekrümmt

Typen von Exponentialfunktionen

👉 Einfache Exponentialfunktion [f(x)=a^x]

Erweiterte Exponentialfunktion [f(x)=ab^x]=> 👉 qck

👉 Allgemeine Exponentialfunktion [f(x)=ab^(mx+n)]

👉 e-Funktion [f(x)=e^x]

Anwendungen

Die Exponentialfunktion passt auf viele Wachstums- und Abnahmeprozesse. Typische Beispiele sind die Radioaktivität, die Ausbreitung von Krankheiten, das Abkühlen von Flüssigkeiten oder das Aufladen eines elektrischen Kondensators. Die Basis a wird dann als Wachstumsfaktor interpretiert.