Basiswissen

Kurzdefinition

• Allgemeiner Bauplan: f(x) = a·eᵀᵉʳᵐ ᵐⁱᵗ ˣ
  

• Wichtig: Das e ist die Basis einer Potenz.
  

• Wichtig: Das x steht im Exponenten der Potenz.
  

Erläuterung

• Die e-Funktion ist eine spezielle Exponentialfunktion:
  

• Eine Funktion der Form "a hoch x" nennt man eine Exponentialfunktion.
  

• a ist ein Platzhalter für eine beliebige reelle Zahl.
  

• Das a nennt man auch die Basis, das x ist hier der Exponent.
  

• Ist die Basis a die Eulersche Zahl e, spricht man von der e-Funktion.
  

• e ist ungefähr 2,71828, mehr unter Eulersche Zahl ↗
  

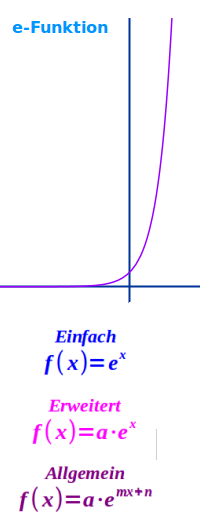
Typen

• ^ ist das Hochzeichen: e^x = eˣ
  

• f(x)=e^x nennt man die einfache e-Funktion ↗
  

• f(x)=a·e^x nennt man die erweiterte e-Funktion ↗
  

• f(x)=a+e^(mx+b) nennt man die allgemeine e-Funktion ↗
  

• Weitere Typen unter e-Funktionen ↗
  

Eigenschaften der einfachen e-Funktion

• y-Achsenabschnitt (0|1)
  

• Es gibt keine Nullstellen.
  

• Es gibt keine Hoch- oder Tiefpunkte.
  

• Es gibt keine Wende- oder Sattelpunkte.
  

• Die erste Ableitung von f(x)=e^x ist f(x)=e^x.
  

• Die Steigung ist an jeder Stelle gleich dem y-Wert.
  

Besonderheit

• Das Besondere an der einfachen e-Funktion ist folgende Eigenschaft:
  

• An jedem Punkt auf dem Funktionsgraphen ist die Steigung f'(x) ...
  

• vom Zahlenwert immer genau dasselbe wie der y-Wert an diesem Punkt.
  

• Man kann kurz formulieren: f'(x) = f(x)
  

Praktische Bedeutung

Synonyme

• Natürliche Exponentialfunktion ↗
  

• e-Funktion ↗