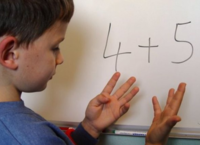Dyskalkulie erkennen
Anzeichen
© 2016
- 2026
Basiswissen|
Zählendes Rechnen|
Kein sicherer Blitzblick|
Keine Mengenkonstanz|
Rechnen dauert sehr lange|
Kein Bündeln|
Fingerrechnen|
Zehnerübertritt ist schwer|
Rückwärtszählen ist schwer|
Kein Baustein-Denken mit Zahlen|
Oft eins daneben|
Zahlendreher sind häufig|
Plusminus-Vertauscher|
Paradoxe Fähigkeiten|
Messen ist schwierig|
Die Zeigeruhr ist sehr schwierig|
Lagewörter sind schwierig|
Einkaufen macht Angst|
Üben bringt nichts|
Textaufgaben sind ein Horror|
Was ist eine Pseudodyskalkulie?|
Was kann man tun, um zu helfen?
Basiswissen
Dyskalkulie kann von erfahrenen Lehrern sicher ab der zweiten Klasse erkannt werden. In älteren Büchern findet man auch noch das sehr passende Wort vom mechanischen Rechnen. Das wichtigste Merkmal zur Erkennung: de Kinder lösen sich nicht vom zählenden Rechnen. Hier stehen noch mehr solche Anzeichen für eine mögliche Dyskalkulie.
Zählendes Rechnen
Dies ist das wichtigste Erkennungszeichen: spätestens gegen Ende des ersten Schuljahres sollte sich ein Kind vom rein zählenden Rechnen lösen. Rechnet es dann noch Aufgaben wie 5+3 indem es in Einerschritten hochzählt, sollte man genauer hinsehen. Siehe auch 👉 Zählen
Kein sicherer Blitzblick
Man legt drei Spielsteine irgendwie auf den Tisch. Die meisten Kinder erkennen sofort und ohne zu zählen die richtige Anzahl. Anzahlen auf einen Blick richtig zu erkennen nennt man in der Didaktik Subitizing. Auf Deutsch könnte man es Blitzblick nennen. Die meisten Menschen beherrschen den Blitzblick oft gut bis zu einer Anzahl von sechs oder sieben. Unbewusst gruppieren sie dazu die Gegenstände: erkennt man zum Beispiel zwei Dreierpäckchen, dann weiß man sofort, dass man insgesamt sechs hat. Kinder mit einer Dyskalkulie haben diese Fähigkeit oft zunächst gar nicht oder nur sehr schwach entwickelt. Lies mehr unter 👉 Blitzblick
Keine Mengenkonstanz
Man legt 4 Steine auf den Tisch und lässt ein Kind die Steine zählen. Dann verschiebt man einen der Steine ein kleines Stückchen an eine andere Stelle und fragt neu: wenn das Kind jetzt neu zählt, fehlt die Idee der sogenannten 👉 Mengenkonstanz (Grundschule)
Rechnen dauert sehr lange
Eines der sichersten Erkennungszeichen für eine Dyskalkulie ist die lange Zeit, die Kinder für eine Lösung brauchen. Wenn zum Beispiel die Aufgabe 20 minus 9 auch gegen Ende des ersten Schuljahres noch länger als 2 Sekunden dauert, dann rechnet das Kind wahrscheinlich zählend. Viele Eltern denken dann, dass das Kind die Aufgabe ja an sich kann, aber halt nur viel Zeit benötigt. Siehe auch 👉 Blitzrechnen
Kein Bündeln
3 und 2 gibt zusammen eine 5: viele Kindern entwickeln spätestens zum Ende der ersten Klasse hin die Grundidee, dass man bestimmte Zahlen zu immer gleichen und handlichen Zahlenbündeln zusammenpacken kann. Sie rechnen 10+3+2 nicht schrittweise über 10+3 und dann am Ende noch 2 dazu. Sie rechnen sofort 10+5. Kinder mit einer Dyskalkulie machen das nicht automatisch von sich aus. Siehe auch 👉 Bündeln
Fingerrechnen
Ein Kind rechnet gegen Ende der ersten Klasse auch einfache Aufgaben wie 10-2 noch mit alternativlos Fingern: schauen Sie dann nach, ob auch "längere" Aufgaben wie 20-9 noch mit Fingern oder zählend gerechnet werden. Wenn ja, ist das ein starkes Zeichen für eine Dyskalkulie. Verteufeln oder verbieten Sie aber auf keinen Fall das Fingerrechnen. Es ist slebst für gute Erwachsene ein oft interessantes Hilfsmittel, es darf aber aber auf Dauer nicht der einzige Weg zum Rechenergebnis bleiben. Lies mehr dazu unter 👉 Fingerrechnen
Zehnerübertritt ist schwer
7+5 oder 21-2 bereiten Probleme: immer wenn es um einen neuen Zehner geht, wird es knifflig. Klappt das im Zahlenraum bis 20 gut, sollte man genau hinsehen, ob das Problem bis 100 erneut auftritt: 82-10 oder 82-13 könnte dann Probleme bereiten. Siehe auch 👉 Zehnerübertritt
Rückwärtszählen ist schwer
Können Sie schnell und sicher das Alphabet rückwärts aufsagen? Welcher Buchstabe kommt direkt vor dem R? Wenn Sie das schwierig finden können Sie vielleicht die Probleme nachempfinden, die jüngere Kinder mit Dyskalkulie beim Rückwärtszählen haben. Sie übertragen nicht automatisch die Logik vom Rückwärtszählen 9-8-7-6 und so weiter auf den Zahlenbereich 20, also auf 19-18-17-16 und so weiter. Beide Rückwärtsketten sind für sie zwei ganz voneinander unabhängige Logiken, die sie getrennt voneinander auswendig lernen. Das zu besprechen, ist eine der wichtigsten Dinge im Rechnen im Zahlenraum bis zwangzig, siehe mehr dazu unter 👉 Rückwärtszählen
Kein Baustein-Denken mit Zahlen
Wenn 9+1 zusammen 10 gibt, dann ist es logisch, dass 10-1 wieder die 9 geben muss: diese Logik teilen nicht alle Kinder. Kinder mit einer Dyskalkulie haben diesen Schluss nicht sicher verinnerlicht. Dass man Zahlen als eine Art Bausteinmuster auffassen kann, ist für sie nicht selbstverständlich. Das anzulegen kann Monate dauern. Ein wichtigster erster Schritt dazu ist das Denken mit den sogenannten 👉 Passerzahlen
Oft eins daneben
12+5=18 oder 21-3=19: Kinder mit einer Dyskalkulie liegen oft genau eins neben dem richtigen Ergebnis. Ein häufiger Grund ist falsches Fingerzählen. Bei 21 minus 3 fangen die Kinder an, bei der 21 zu zählen und halten dann den ersten Finger hoch. Dann kommt die 20 mit dem zweiten Finger und am Ende die 19 mit dem dritten Finger. Also sagen sie folgerichtig: 21 minus 3 gibt 19. Der Fehler ist, dass man bei der 21 noch keinen Finger hochhalten darf. Die korrekte Methode wäre mit richtiger Sprechweise wäre: 21! minus 1 - jetzt einen Finger hochhalten - gibt 20. Noch einmal minus 1 - zweiten Finger hoch - gibt 19. Und noch einmal minus 1 - dritter Finger hoch - gibt 18. Der Grundfehler ist, dass man beim zählenden Plus- oder Minusrechnen mit der 0 anfangen muss. Eng verwandet damit sind auch die Probleme beim messen von Strecken mit einem 👉 Lineal
Zahlendreher sind häufig
45 wird zu vierundfünfzig: auch viele Erwachsene, etwa auch gute Mathematiker und Rechner, machen manchmal Zahlendreher-Fehler. Wenn aber Kinder diesen Fehler häufig machen, etwa auch beim Abschreiben von Rechenaufgaben, dann sollte man genauer hinsehen. Es dauert oft Monate, die Zahlendreher durch Üben zu verringern. Passieren sie beim Abschreiben von Rechenaufgaben, können sie erheblich die Noten von Test verschlechtern. Siehe auch 👉 Zahlendreher
Plusminus-Vertauscher
Im Buch steht die Aufgaben 20-5 und die Kinder übertragen sie als 20+5 in ihr Lösungsheft. Dieser Fehler ist bei manchen Kindern sehr häufig und auch sehr hartnäckig. Es gibt Tipps, wie man ihm aber besiegen kann. Siehe dazu unter 👉 Plusminus-Vertauscher
Paradoxe Fähigkeiten
428 minus 216 wird sofort richtig gelöst, aber 401 minus 2 ist ein Riesenproblem. Wie kann das sein? Die Antwort ist, dass die Kinder im Kopf schriftlich rechnen. Sie schreiben im inneren Auge oben die 428 auf und direkt darunter die 216. Dann rechnen sie von rechts nach links schriftlich minus im Kopf. Dabei gehen sie Ziffer für Ziffer vor. Solange man sich keinen Übertrag merken muss, ist diese Methode schnell und sicher. Wer damit aber 401 minus 2 rechnen will, kriegt große Probleme mit dem Übertrag. Kinder die sich an schriftlichen Rechenmethoden festklammern haben oft eine Dyskalkulie. Siehe auch 👉 schriftlich rechnen
Messen ist schwierig
Bis hin in die Oberstufe kann das Messen von zum Beispiel Längen mit dem Lineal oder das Ablesen von Sekunden und Minuten auf einer Stoppuhr mit Zeigern schwer sein: die Kinder legen das Lineal falsch an und liegen dann oft einen Zentimeter daneben. Legen sie zum Beispiel ein Lineal an, fangen sie die Zentimetermarken bei der 0 an zu zählen, sprechen aber bei der Null schon die Zahl 1. So werden die gemessenen Längen systematisch ein Zentimeter zu lang. Der tiefere Grund ist hier ein Unverständnis der kardinalen gegenüber der bevorzugten ordinalen Idee von Zahlen. Siehe dazu auch 👉 Lineal
Die Zeigeruhr ist sehr schwierig
Ein fast zu 100 % sicheres Anzeichen für eine Dyskalkulie ist es, wenn Kinder auffällig große Probleme mit der Zeigeruhr haben. Viertel vor neun oder halb fünf ist für sie oft genauso unverständlich wie 10 nach 8. Sieht man genauer hin, entdeckt man oft Unsicherheiten bei Lagewörtern: nach, vor, zwischen, hinter und ähnliche Worte sind nicht klar verstanden. Siehe auch 👉 Zeigeruhr
Lagewörter sind schwierig
Einem Schüler der Klasse vier bereite folgende Aufgabe über Wochen hinweg immer wieder Probleme. Auf dem Tisch standen in einiger Entfernung zwei Tiere, zum Beispiel ein Affe und ein Hase. Dann sollte ein drittes Tier zwischen den Affen und den Hasen gestellt werden. Der Junge war sich immer wieder unsicher was das bedeutete. Es dauerte gut 2 Jahre die Unsicherheit mit solchen Ort- und Zeitworten zu klären. Bei älteren Kindern schwierig sind dann zum Beispiel Worte wie entlang, senkrecht oder querab. Für eine Liste solcher Worte siehe unter 👉 Lagewörter
Einkaufen macht Angst
Geht ein Kind aber der Klasse 3 mit Bargeld nicht gerne einkaufen, hängt es vielleicht damit zusammen, dass es unsicher mit dem Wechelgeld ist. Uns berichten auch Erwachsene Menschen mit Dyskalkulie davon, dass sie nie ohne Taschenrechner einkaufen gehen. Siehe auch 👉 Wechselgeld
Üben bringt nichts
Uns berichten viele Eltern, dass sie oft stundenlang über Wochen immer dieselbe Aufgabentypen geübt haben, am Ende aber nichts hängen bleibt. Nach der Arbeit "ist alles weg". Das betrifft fast alle Aufgabentypen. Fachleute planen zum Beispiel für das Lernen des Einspluseins und des Einmaleins mehrere Jahre ein. Siehe auch 👉 Einmaleins
Textaufgaben sind ein Horror
Das gilt nicht nur für Kinder mit einer Dyskalkulie, für diese aber ganz besonders: Das kann mindestens zwei Gründe haben. Kinder mit einer Dyskalkulie haben a) oft auch eine leichte oder starke Legasthenie. Sie benötigen dann extrem viel mehr Zeit zum Lesen einer Aufgabenstellung als andere Kinder. Zum Rechnen fehlt dann oft die Zeit. Und b) Kinder mit einer Dyskalkulie haben oft kein sicheres Verständnis von Lagewörtern. Kommen diese in Texten vor, wissen die Kinder dann nicht mehr weiter. Siehe dazu auch 👉 Textaufgaben lösen
Was ist eine Pseudodyskalkulie?
Seit etwa 2015 stellen wir allen neuen Schülern (auch Studenten) in einer Probestunde die Rechenaufgaben: was ist 712 geteilt durch 4? Etwa die Hälfte der Schüler zeigt dabei Unsicherheiten. Gut ein Viertel kann die Aufgabe auch nach längerem Überlegen überhaupt nicht lösen. Was verwundert ist, dass auch Schüler mit einer 1 oder 2 in Mathe, selbst im LK, damit Probleme haben können. Diese Probleme verschwinden aber sofort, wenn man ihnen einen einfachen Rechenweg zeigt. Hat jemand extreme Rechenprobleme, die aber nach wenigen Erklärungen schnell und dauerhaft verschwinden, dann sprechen wir von einer 👉 Pseudodyskalkulie
Was kann man tun, um zu helfen?
Das Wichtigste: wenn man es langfristig angeht, kann jedes Kind mit Dyskalkulie normal gut in Mathematik und Schulfächern mit Zahlen mitkommen. Wichtig sind Geduld, Zuversicht und eine professionelle Lernmethode. Siehe dazu auch 👉 Dyskalkulie Elterntipps