A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Quantelung

Physik

© 2016 - 2025


Basiswissen｜ Einführung: die gequantelte Rutschbahn｜ Die Anfänge der Quantenphysik｜ 1900: Die Geburt der Quantelung in der modernen Physik｜ 1905: Einsteins Lichtquantenhypothese｜ 1911-1914: Franck-Hertz-Versuch｜ 1913: Bohrsches Atommodell｜ 1913: Millikans Elementarladung｜ 1921 bis 1926: der Elektronenspin｜ Quantelung und Quantisierung｜ Zwei Arten der Quantelung｜ Quaestiones｜ Fußnoten


Basiswissen


Als Quantelung bezeichnet man in der Physik die Tatsache, dass eine physikalische Größe, etwa der Abstand eines Elektrons in einem Atom hin zum Atomkern[1] für stabile Zustände[10] nur bestimmte Werte annehmen kann, Zwischenwerte aber keinen stabilen Zustände ergeben. Und: eine physikalische Größe kann nur ganzzahlige Vielfache von einer konstanten kleinsten Grundmenge annehmen, dem sogenannten Quant.[8] Das ist hier kurz mit Beispielen vorgestellt.



Bildbeschreibung und Urheberrecht
Im Bohrschen Atommodell (links) gibt es für Elektronen um den Kern von Atomen nur ausgewählte erlaubte Abstände. Das ist aus Sicht der klassischen Physik genauso unerklärlich wie eine Rutschbahn, bei der man immer nur genau eine von vier verschiedenen Geschwindigkeiten haben kann, egal wie schnell man am Anfang darauf springt, wie stark man unterwegs bremst oder wie steil die Abschnitte der Bahn sind. Wie sehen dann Wechsel zwischen zwei Geschwindigkeiten aus? Schlagartig? Und hat man beim Start schlagartig die Geschwindigkeitsstufe 1, ohne Zwischengeschwindigkeiten? Und wie sieht Bremsen aus, wenn es zwischen der Geschwindigkeit 3 und 2 keine Zwischenwerte geben darf? Und was genau legt fest welche Geschwindigkeiten stabil eingenommen werden können und welche nicht? Gibt es eine tiefere Logik? Fragen dieser Art wurden im Zusammenhang mit dem weiter entwickelten Bohrschen Atommodell in den 1920er Jahren von Physikern disktutiert. © JabberWork Gunter Heim/ChatGPT ☛


Einführung: die gequantelte Rutschbahn


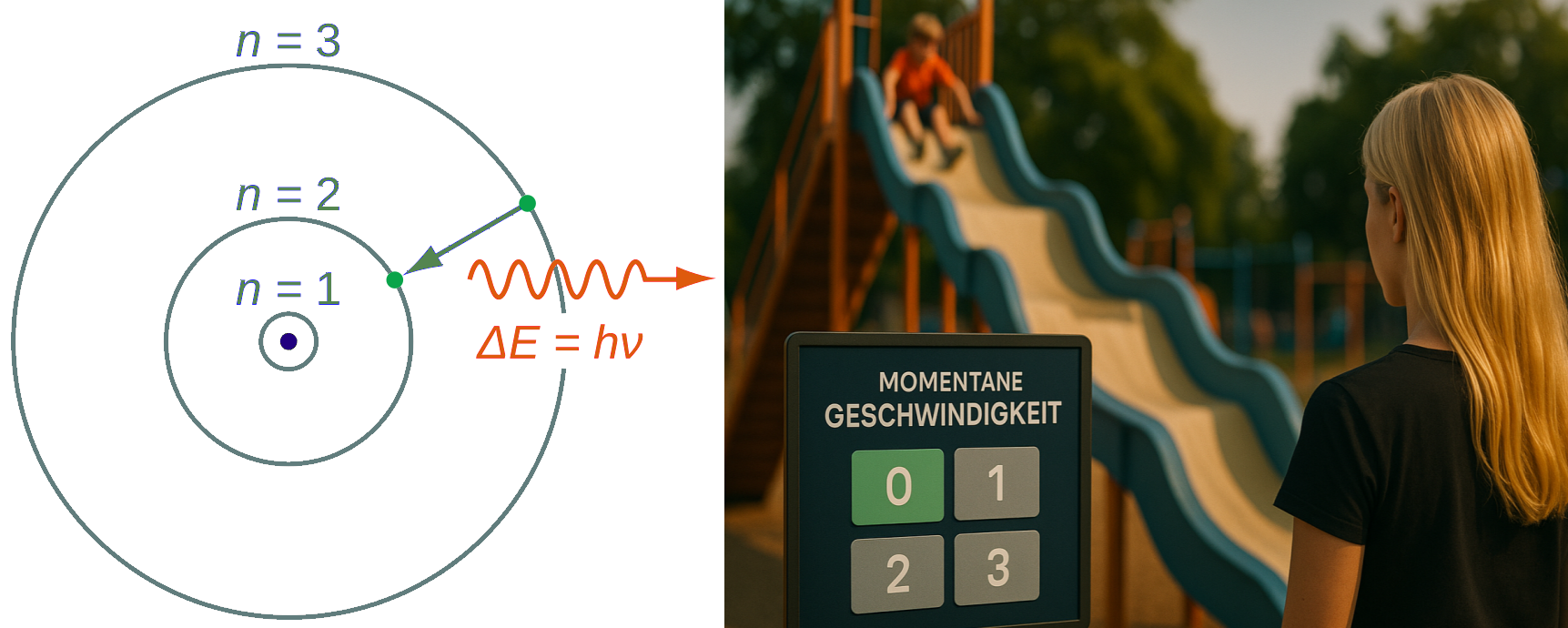
Die Idee der Quantelung war im frühen 20ten Jahrhundert ein gewaltiger Denkwiderstand für Physiker. Aber warum ist es so schwer oder wenig akzeptabel, sich eine Quantelung von physikalischen Größen vorzustellen. Vielleicht wird das an einem fiktiven Beispiel deutlich: die gequantelte Rutschbahn.

Stellen wir uns eine ganz normale Rutschbahn auf einem Spielplatz vor. Ein Kind setzt sich oben auf die Bahn und rutscht herunter. In unserem Gedankenexperiment können wir die Rutschbahn nun in beliebig feinen Abstufungen auch steiler machen oder flacher. Damit sollte theoretisch auch die Geschwindigkeit zu- oder abnehmen, mit der die Kinder herunterrutschen. Wenn zu jeder Steilheit der Rutsche genau eine Rutschgeschwindigkeit gehört, die bei keiner anderen Steilheit auftritt, dann wäre die Rutschgewindigkeit nicht gequantelt. Sie wäre eine sogenannte kontinuierliche Größe. Zwischen der Rutschgewindigkeit 1 m/s und 2 m/s gibt es unendlich viele Zwischengeschwindigkeiten, die ein Kind einnehmen könnte.

Jetzt stellen wir uns die Rutschgeschwindigkeit gequantelt vor: ganz gleich wie steil die Rutschbahn auch ist, die mögliche Geschwindigkeit, mit der ein Kind rutschen kann, muss immer ein ganzzahliges Vielfaches von 0,5 m/s sein. Möglich sind dann also die Geschwindigkeiten wie 0 m/s, 0,5 m/s, 1,0 m/s, 1,5 m/s oder auch 2,0 m/s und so weiter. Völlig unmöglich aber wäre zum Beispiel eine Geschwindigkeit von 0,4 m/s oder von 1,95 m/s. Diese Quantelung wirft dann verschiedene interessante Fragen auf:

  • Wenn man bei einem Neigungswinkel der Rutschbahn von z. B. 20° eine Geschwindigkeit von 0,5 m/s hätte, wenn Geschwindigkeit hätte ein Kind dann bei einer Steilheit von nur 10°? Würde es gar nicht rutschen? Würde es die 0,5 m/s haben? Ab welcher Steilheit der Rutsche würde das Kind überhaupt rutschen können?
  • Wenn während des Rutschens die Rutsche steiler gestellt wird, man denke an ein Fahrgeschäft auf einer Kirmes, ändert sich die Rutschgeschwindigkeit die schlagartig (Quantensprung) oder zumindest in einer sehr kurzen Zeit kontinuierlich?
  • Kann es eine Rutschbewegung immer nur bei ganz genau definierten Neigungswinkeln geben? Oder führt jeder beliebige Neigungswinkel zu irgendeiner der erlaubten Geschwindigkeiten?

Wenn man einmal versucht, in Gedanken diese Rutschbahn möglichst anschaulich mit möglichst konkreten Bilder zu denken, wird man ganz von alleine auf die Folgen und weitere interessante Fragen stoßen, die mit einer Quantelung von Größen einhergehen.

Die Anfänge der Quantenphysik


Bis zum Jahr 1900 ging man davon aus, dass viele physikalische Größen sowohl rechnerisch wie auch real in der Natur beliebig fein stückelbar sind. So nahm man damals zum Beispiel nicht an, dass es so etwas wie Energie-Atome gäbe, also kleinste Mengen an Energie, die in bestimmten Versuchsanordnungen prinzipiell nicht weiter unterteilt werden können. Dass man aber genau in diese Richtung denken müsste, erzwangen die Befunde verschiedener Versuche.

1900: Die Geburt der Quantelung in der modernen Physik


Im Jahr 1900 entdeckte der Physiker Max Planck (1858 bis 1947), dass Energien möglicherweise gequantelt gedacht werden müssen. Im Zusammenhang mit einem sogenannten Schwarzen Strahler versuchte er die damals bekannten Naturgesetze in einen zahlenmäßigen Zusammenhang zu bringen. Dabei formulierte er noch vorsichtig die Idee, dass Energiemengen nur in eine bestimmte, endliche Anzahl von gleichen "Energieelementen" zerlegt werden könnte:

ZITAT:

Max Planck, 1900: "Nun ist noch die Verteilung der Energie auf die einzelnen Resonatoren innerhalb jeder Gattung vorzunehmen, zuerst die Verteilung der Energie E auf die N Resonatoren mit der Schwingunszahl ν. Wenn E als unbeschränkt teilbare Grösse angesehen wird, ist die Verteilung auf unendlich viele Arten möglich. Wir betrachten aber - und dies ist der wesentliche Punkt der ganzen Berechnung - E als zusammengesetzt aus einer ganz bestimmten Anzahl endlicher gleicher Teile und bedienen uns dazu der Naturconstanten h=6,55.10⁻²⁷ [erg x sec]. Diese Constante mit der gemeinsamen Schwingungszahl ν der Resonatoren multiplicirt ergiebt das Energieelement ε in erg, und durch Division von E durch ε erhalten wir die Anzahl P der Energieelemente, welche unter die N Resonatoren zu verteilen sind. Wenn der so berechnete Quotient keine ganze Zahl ist, so nehme man für P eine in der Nähe gelegene ganze Zahl."[12]

Dieser Gedanke war revolutionär. Max Planck selbst weist in keinem seiner Veröffentlichtungen aus der Zeit um 1900[12][13] auf die enorme Tragweite seines Gedankens hin. Energie, die man bis dahin als stufenlos teilbar hielt, scheint als zumindest unter bestimmten Umständen nur gestückelt, das heißt gequantelt, übergehen zu können.

1905: Einsteins Lichtquantenhypothese


Im Jahr 1905 entwickelte Albert Einstein (1857 bis 1955) daraus seine Lichtquantenhypothese[9]: Licht breitet sich im Raum in Form von eng begrenzten (lokalisierten) Einheiten von Energie aus. Und diese können nur in Gänze, also ungeteilt, aufgenommen oder abgegeben werden. Es war dieser Gedanke Einsteins, nicht seine Relativitätstheorie, die ihm später den Nobelpreis einbrachte. Siehe mehr unter Lichtquant ↗

1911-1914: Franck-Hertz-Versuch


In der Zeit zwischen 1911 und 1914, kurz vor Ausbruch des ersten Weltkriegs, führten die Physik James Franck und Gustav Hertz Versuche durch[13] bei denen sie zeigten, dass Elektronen ihre Bewegungsenergie nur in festen Energiepaketen an Atome abgeben können. Oder besser gesagt: die Atome nehmen die Energie entweder in Paketen vorgegebener Menge oder gar nicht auf. Später deuteten Franck und Hertz die Befunde auch im Sinne der neu entstehenenden Quantenphysik.[15] Gequantelt ist die hier Energiemenge, die ein Atom aufnimmt. Im Zusammenhang mit dem Franck-Hertz-Versuch spricht man auch von einer "quantenhaften Energieabsorption"[19] oder von "quantisierten Energien im Atom"[20]. Siehe auch Franck-Hertz-Versuch ↗

1913: Bohrsches Atommodell


Es war der Schwede Niels Bohr, der seit dem Jahr 1913[16] ein Modell von Atomen entwickelte, das die Befunde von Franck und Hertz aber auch viele weitere empirische Fakten aus der Spektralanalyse von Atomen, aufgriff und mit einer Quantelung von inneren Zuständen der Energien im Atom erklärte. 1913 schrieb er:

ZITAT:

"Wenn wir also annehmen, dass die Umlaufbahn eines Elektrons in einem stationären Zustand kreisförmig ist […], liegt den Ergebnissen der Berechnungen die einfache Bedingung zugrunde, dass das Bahndrehmoment (angular momentum) des Elektrons um den Kern in einem stabilen Zustand ein ganzzahliges Vielfaches eines universellen Wertes ist, unabhängig von der Ladungszahl des Atomkerns."[21]

In seiner Veröffentlichung von 1913 spricht Bohr audrücklich von einer Quantentheory (quantum theory) und verweist auf die Vorarbeiten von Planck und vielen anderen Wissenschaftlern. Bohr unterstreicht, dass eine Quantelung in der klassischen Elektrodynamik von Maxwell keinen Platz hatte.[22][23]

1913: Millikans Elementarladung


Im Jahr 1913 konnte R. A. Millikan die Elementarladung des Elektrons recht genau bestimmen.[18] Man beobachtet nirgendwo in der Natur Mengen an elektrischer Ladung, die kleiner sind als diese Elementarladung. Damit kann man sagen, dass auch die elektrische Ladung gequantelt ist. Siehe auch Elementarladung ↗

1921 bis 1926: der Elektronenspin


Schon Niels Bohr hatte 1913 vermutet, dass der Bahndrehimpuls von Elektronen im Atom gequantelt sein könnte.[16] Der Bahndrehimpuls bezieht sich auf die Bewegung eines Körpers auf einer mehr oder minder kreisförmigen Bahn. Es gibt aber auch einen Drehimpuls der aus einer Rotation eines Körpers um sich selbst resultiert. Seit 1921 aber gab es Hinweise, dass dieser Drehimpuls bei Elektronen gequantelt sein könnte.[17] Man muss sich immer wieder deutlich machen, was das Wort Quantelung in einem bestimmten Zusammenhang meint: es besagt hier, dass sich Elektronen in bestimmten Anordnungen nur mit bestimmten Drehzahlen um sich selbst drehen können, andere Drehzahlen aber nicht erlaubt sind. Diese Rotation um sich selbst bezeichnet man auch als Spin ↗

Quantelung und Quantisierung


Das Wort Quantelung bezieht sich auf als real gedachte Dinge der Wirklichkeit. Energie kann gequantelt sein oder auch ein Drehimpuls. Als Quantisierung hingegen bezeichnet man einen gedanklichen Prozess der geistigen Arbeit, bei dem eine Naturbeschreibung aus gequantelt gedachten Größen entsteht. Die Unterscheidung ist eine ähnlich wie die zwischen Farbe und Färben. Das eine ist eine Eigenschaft der Wirklichkeit, das andere eine Handlung. Siehe mehr unter Quantisierung ↗

Zwei Arten der Quantelung


Man kann zwei Arten der Quantelung unterscheiden: eine universelle Quantelung wie die der beobachtbaren Menge an elektrischer Ladung. Elektrische Ladung tritt uns messbar immer nur als ganzzahlige Vielfache von e, der sogenannten Elementarladung entgegen. Ganz egal, ob man Ladung in einem Atom, auf einem Tropfen Öl oder in einen schwarzen Loch bestimmt: immer ist das das Soundsovielfache der kleinstmöglichen Ladungsmenge e. Anders sieht es mit Energiezuständen in einem Atom aus. Hier sind die Energiezustände immer ganzzahlige Vielfache einer kleinsten Energiemenge, aber diese kleinste Energiemenge hängt vom betrachteten Atom ab. Man könnte hier von einer systemgebundenen Quantelung sprechen, im Gegensatz zu einer universellen Quantelung.

Quaestiones


  • 1) Elektrische Ladung gilt als eine gequantelte Größe. Tatsächlich gibt es eine kleinste, elementare Menge elektrischer Ladung, die Elementarladung. Gleichzeitig sagt man auch, dass Energie, etwa in den Zuständen von Atomen gequantelt ist. Doch zwischen diesen beiden Arten von Quantelung gibt es doch einen qualitativen Unterschied: bei der Ladungsmenge gibt es eine absolut geltende kleinste Einheit, sozusagen eine universell kleinste Ladungsmenge. Das gibt es bei Enegie nicht. Hier hängen die erlaubten Werte der Gesamtenergie jeweils von der spezifischen Situation ab, etwa welche Atom man betrachtet oder bei der Energie von Photonen, welche Frequenz ein Photon hat. Werden diese zwei unterschiedlichen Arten von Quantelung in der Literatur unterschieden? Gibt es etablierte Fachbegriffe - egal in welcher Sprache - zur Differenzierung? Gibt es zitierfähige Fachartikel, die sich mit genau diesem Aspekt der Quantentheorie beschäftigen?
  • 2) Wozu sind physikalische Größen überhaupt gequantelt? Mit dieser Frage verlässt man die Physik als empirische Naturwissenschaft und begibt sich in das Gebiet philosophischer Spekulationen. Warum soll die Energie in einem bestimmten Atom nicht beliebige Werte annehmen können? Wie sähe ein Universum aus, in dem das möglich wäre? Ein möglicher Zweck einer Quantelung könnte sein, dass das Universum in Analogie zu einer Computersimulation zu verstehen ist, in der die Simulation nur diskrete Werte erlaubt, etwa um den Raum der möglichen Zustände so weit einzuschränken, dass die "Rechenleistung" des Simulators nicht überstrapaziert wird. Siehe dazu auch Simulationshypothese ↗

Fußnoten


  • [2] Das Aufrunden ist eine von mehreren Arten, Zahlen zu runden. Es wurde hier gewählt, weil die Regeln dazu recht leicht zu verstehen sind. Siehe allgemein auch den Artikel zum Runden ↗
  • [3] Als reell bezeichnet man jede Zahl, die man sich irgendwo auf einer Zahlengeraden vorstellen kann. Vor allem ist jede Zahl in einer beliebigen Kommadarstellung eine reelle Zahl ↗
  • [4] Ganz nennt man jede Zahl, die als Dezimalzahl geschrieben kein Komma benötigt. Siehe mehr unter ganze Zahl ↗
  • [5] Man sagt, die reellen Zahlen sind kontinuierlich, die Abstände zwischen ihnen können beliebig klein gemacht werden. Siehe mehr unter Kontinuum ↗
  • [6] Diskret nennt man Zahlen, wenn es eine Mindestabstand zwischen ihnen gibt, der nicht unterschritten werden kann. Siehe mehr unter Diskretheit ↗
  • [7] Menschen können nicht anders als in Raum, Zeit und Kausalität zu denken. Doch ob es in der Wirklichkeit auch Raum, Zeit und Kausalität geben muss, ist Kant zufolge damit noch nicht gesagt. Siehe mehr zu diesem Gedanken im Artikel zum Ding an sich ↗
  • [8] "Quantelung ist die Eigenschaft, dass ganz verschiedene physikalische Größen (Energie, Drehimpuls, Ladung) Vielfaches eines kleinsten (diskreten) Betrages sind, dem Quant." In: der Artikel "Quantentheorie". Spektrum Lexikon der Astronomie. Stand 19. Oktober 2024. Online: https://www.spektrum.de/lexikon/astronomie/quantentheorie/375
  • [9] Albert Einstein im Jahr 1905 über Energiequanten: "Es scheint mir nun in der Tat, daß die Beobachtungen über die 'schwarze Strahlung', Photoluminiszenz, die Erzeugung von Kathodenstrahlen durch ultraviolettes Licht und andere die Erzeugung bez. Verwandlung des Lichtes betreffende Erscheinungsgruppen besser verständlich erscheinen unter der Annahme, daß die Energie des Lichtes diskontinuierlich im Raume verteilt sei. Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahles die Energie nicht kontinuierlich auf größer und größer werdende Räume verteilt, sondern es besteht dieselbe aus einer endlichen Zahl von in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen und nur als Ganze absorbiert und erzeugt werden können." In: Annalen der Physik. Band 322, Nr. 6, 1905, S. 132–148, doi:10.1002/andp.19053220607. Dort die Seite 133. Mehr unter Lichtquantenhypothese [Einstein] ↗
  • [10] In den 1920er Jahren wurden noch vermutet, dass Elektronen im Atom überhaupt keinen Zwischenzustand zwischen zwei erlaubten Zuständen einnehmen könnten, auch nicht für sehr kurze Zeiten. Diese - heute überholte Vorstellung - führte dann zu dem Gedanken, dass Elektronen bei einem Wechsel zwischen zwei stabilen Zuständen ohne Zeitverzug und ohne Zwischenorte direkt vom Anfangs- zum Endzustand springt. Dieser Gedanke ist behandelt im Artikel zum Quantensprung ↗
  • [11] Dass sich das Wort Quantelung direkt auf die Wirklichkeit bezieht, und nicht auf Denkvorgänge zur Beschreibung der Wirklichkeit, zeigt beispielhaft ein Artikel von Enrico Fermi aus dem Jahr 1926: Enrico Fermi: Zur Quantelung des idealen einatomigen Gases. Z. Physik 36, 902–912 (1926). https://doi.org/10.1007/BF01400221
  • [12] Max Planck: Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum. In: Verhandl. Dtsch. Phys. Ges. Band 2, 1900, S. 237–245.
  • [13] Max Planck: Über das Gesetz der Energieverteilung im Normalspektrum. Annalen der Physik, Bd. 4, 1901, S. 553–563.
  • [17] Zur Quantelung des Elektronenspins: "So far as we know, the idea of a quantised spinning of the electron was put forward for the first time by A. K. Compton (Journ. Frankl. Inst., Aug. 1921, p. 145), who pointed out the possible bearing of this idea on the origin of the natural unit of magnetism. Without being aware of Compton's suggestion, we have directed attention in a recent note (Naturwissenschaften, Nov. 20, 1925) to the possibility of applying the spinning electron to interpret a number of features of the quantum theory of the Zeeman effect..." In: G. Uhlenbeck, Samuel Goudsmit: Spinning Electrons and the Structure of Spectra. Nature 117, 264–265 (1926). Online: https://doi.org/10.1038/117264a0
  • [18] R. A. Millikan: On the Elementary Electrical Charge and the Avogadro Constant). Physical Review. Series II. 2 (2): 109–143. (1913). Online: DOI: doi:10.1103/PhysRev.2.109.
  • [19] Dorn.Bader. Physik SII Gesamtband Gymnasium. Westermann Bildungsmedien. Braunschweig. 2023. ISBN: 978-3-14-152376-8. Die "quantenhafte Energiebsorption" im Zusammenhang mit dem Frack-Hertz-Versuch wird behandelt auf den Seiten 418 und 419.
  • [20] Metzler Physik. 5. Auflage. 592 Seiten. Westermann Verlag. 2022. ISBN: 978-3-14-100100-6. Unter dem Stichwort "Quantisierte Energien im Atom" heißt es zur Bedeutung des Franck-Hertz-Versuchs: "Dies bestätigt die Hypothese, dass im Atom nur bestimmte Werte der Energie möglich sind." (Seite 349). Siehe auch Franck-Hertz-Versuch ↗
  • [21] Im Original von 1913: "If we therefore assume that the orbit of the electron in the stationary states is circular, the result of the calculation on p. 5 can be expressed by the simple condition: that the angular momentum of the electron round the nucleus in a stationary state of the system is equal to an entire multiple of a universal value, independent of the charge on the nucleus. The possible importance of the angular momentum it, the discussion of atomic systems in relation to Planck's theory is emphasized by Nicholson." In: Niels Bohr: On the Constitution of Atoms and Molecules, Part I. Philosophical Magazine. 26, 1913, S. 1–25. Dort auf Seite 15. Online: https://uni-tuebingen.de/fileadmin/Uni_Tuebingen/Fakultaeten/MathePhysik/Institute/IAP/Forschung/MOettel/Geburt_QM/bohr_PhilMag_26_1_1913.pdf
  • [22] "The result of the discussion of these questions seems to be a general acknowledgment of the inadequacy of the classical electrodynamics in describing the behaviour of systems of atomic size. Whatever the alteration in the laws of motion of the electrons may be, it seems necessary to introduce in the laws in question a ttnantity foreign to the elassical electrodynamics, i. e. Planck's constant, or as it often is called the elementary quantum of action." In: Niels Bohr: On the Constitution of Atoms and Molecules, Part I. In: Philosophical Magazine. 26, 1913, S. 1–25. Dort auf Seite 2. Online: https://uni-tuebingen.de/fileadmin/Uni_Tuebingen/Fakultaeten/MathePhysik/Institute/IAP/Forschung/MOettel/Geburt_QM/bohr_PhilMag_26_1_1913.pdf
  • [23] "How much the above considerations differ from an interpretation based on the ordinary electrodynamics is perhaps most clearly shown by the fact that we have been forced to assume that a system of electrons will absorb a radiation of a frequency different from the frequency of vibration of the electrons calculated in the ordinary way. It may in this connexion be of interest to mention a generalization of the considerations to which we are led by experiments on the photo-electric effect, and which may be able to throw some light on the problem in question." In: Niels Bohr: On the Constitution of Atoms and Molecules, Part I. In: Philosophical Magazine. 26, 1913, S. 1–25. Dort auf Seite 16. Siehe auch Photoelektrischer Effekt ↗


Quant">