A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

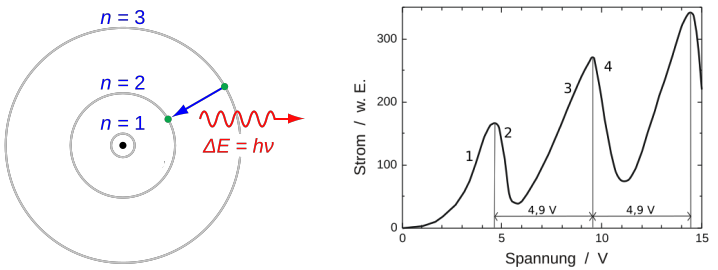
Energiequantelung

Quantenphysik

© 2016 - 2025


Basiswissen｜ Wichtige Formeln｜ Energie und Entropie｜ Elektronen in Atomhüllen｜ Das klassische Planetenmodell｜ Die Spektroskopie im Planetenmodell der Atomhülle｜ Energiequantelung in Atomhüllen｜ Bohrsches Atommodell｜ Franck-Hertz-Versuch｜ Lichtenergie｜ Andere Quantelungen｜ Quantenphilosophisch｜ Das So-Sein der Welt｜ Realität als Simulation｜ Quantelung und Quantisierung｜ Fußnoten


Basiswissen


In der Elektronenhülle eines bestimmten Atoms nehmen die Elektronen Energie nur in festen, vorgegebenen kleinsten Paketen auf und geben sie auch nur in diesen Paketen ab. Und das Atom kennt nur stabile Zustände, die sich um diese gequantelten Mengen an Energie unterscheiden. Die Quantelung von Energie tritt auch bei anderen Vorgängen auf und ist keineswegs logisch. Sie lässt sich aus keiner fundamentaleren Theorie ableiten. Die Quantelung von Energie ist eine der gegebenen Tatsachen der physikalischen Welt.



Bildbeschreibung und Urheberrecht
Links eine typische Skizze zur Darstellung der Energiequantelung in den Elektronenhüllen von Atomen, rechts eine typische Darstellung der Messergebnisse des Franck-Hertz-Versuches © JabberWorks AHellwig ☛


Wichtige Formeln


Formeln

  • E=hf [Lichtquanten]
  • E = h·c:l [Lichtquanten]
  • ΔE=Eₙ-Eₘ [in Atomhüllen]
  • hf=Eₙ-Eₘ [kombiniert]

Legende

  • Eₙ = die Energie des höheren Energiezustandes
  • Eₘ = die Energie des niedrigeren Energiezustandes

Energie und Entropie


Bereits vor der Entstehung der eigentlichen Quantenphysik ab dem Jahr 1900 vermutete bereits 1891 der Physiker und Wegbereiter der statistischen Betrachtung der kinetischen Gastheorie, der Österreicher Ludwig Boltzmann, dass Energie in kleinsten, nicht mehr weiter teilbaren Energieatomen vorkommen könnten. Den Ausgangspunkt seiner Überlegung war der Wunsch, die Entropie auf eine anschauliche Weise zu fassen. Dazu musste man "zählen", wie viele verschiedene Orte und Geschwindigkeiten jedes einzelne aller Gasteilchen in einem betrachteten Volumen einnehmen können, um letztendlich damit doch auf dieselbe Temperatur zu kommen:

ZITAT:

"Die lebendigen Kräfte gehen continuirlich in einander über".

Lebendige Kraft war der damalige Ausdruck für das, was wir heute kinetische Energie oder Bewegungsenergie nennen. Mit kontinuirlich meinte Boltzmann, dass zwischen zwei verschiedenen Werten der kinetischen Energie eines Gastteilchen unendlich viele Zwischenwerte liegen. Das ist in enger Analogie zu den reellen Zahlen zu sehen: diese füllen lückenlos die Zahlengerade aus und zwischen zwei konkreten Zahlen, etwa der Zahl 1 und der Zahl 4, liegen unendlich viele weitere reelle Zahlen. Wie soll man so etwas zählen? Derart angeordnete Dinge nennt man in der Mathematik und Physik ein Kontinuum ↗

Um das mathematische Problem der Anzahl von Zuständen in einem Kontinuum bestimmen zu müssen überhaupt erst einmal angehen zu können, wich Boltzmann diesem Problem zunächst aus, indem er - rein hypothetisch als Denkmodell - annahm, dass zwischen zwei energetisch verschiedenen Zuständen nur eine begrenzte, endliche Anzahl weiterer Zustände liegen kann:

ZITAT:

"Wir wollen zunächst annehmen, jedes Molekül sei nur im Stande, eine bestimmte endliche Anzahl von Geschwindigkeiten anzunehmen".[16]

Das Analogon aus der Mathematik wäre das Denken in ganzen Zahlen: denkt man nur in ganzen Zahlen, so liegen zwischen der Zahl 1 und der Zahl 4 nicht mehr unendlich viele Zahlen dazwischen, sondern nur noch genau 2: die Zahl 2 und die Zahl 3. Damit konnte Boltzmann erst einmal einfach weiter rechnen. Doch später, im Jahr 1891, erwog Boltzmann durchaus, ob die kinetischen Energien der Gasteilchen nicht doch auch in der Wirklichkeit endlich seien:

ZITAT:

"Ich sehe keinen Grund, nicht auch die Energie als atomistisch eingeteilt zu sehen."[17]

Damit aber hat Boltzmann einen Kerngedanken, oder überhaupt den Kerngedanken der erst neun Jahre später ins Leben gerufenen Quantenphysik vorweg genommen, nämlich die Idee, dass auch scheinbar kontinuierlich gedachte Größen wie Energie atomistisch, das heißt gestückelt oder gequantelt sein könnten.

Elektronen in Atomhüllen


Das klassische Planetenmodell


Das klassische Beispiel für die Quantelung von Energie bietet die Physik der Elektronen in Atomhüllen. Als klassisch bezeichnet man die Physik vor der Quanten- und der Relativitätstheorie. In der klassischen Vorstellung von Elektronen in Atomen umkreisen die Elektronen den Atomkern. Man denkt sich die Elektronen dabei ähnlich wie Planeten, die ihre Sonne umkreisen[10]. In dieser klassischen Vorstellung zieht der positiv geladene Atomkern die negativ geladenen Elektronen an. Um nicht Richtung Atomkern zu wandern, benötigen die Elektronen eine bestimmte Geschwindigkeit auf ihrer Kreisbahn. Diese Geschwindigkeit bewirkt eine nach außen wirkende Zentrifugalkraft, die die Anziehungskräfte des Kerns genau ausgleicht. So wie nun ein Planet bei passender Geschwindigkeit die Sonne in jeder beliebigen Entfernung umkreisen kann, so könnte theoretisch auch ein Elektron den Atomkern in jeder beliebigen Entfernung umkreisen. Das gilt in der klassischen Vorstellung.

Die Spektroskopie im Planetenmodell der Atomhülle


Atome eines bestimmten Elementes senden für dieses Atom ganz bestimmte Lichtfarben aus. Ein Beispiel dafür sind die sogenannten Natriumdampflampen. Die Atome des Elementes Natrium senden nur Licht ein ganz genau definierten Gelbfärbung aus. Man erklärt sich die Aussendung von Licht durch Atome so, dass man der Atomhülle erst Energie zuführt. Das kann in Form von Stößen von außen sein (Franck-Hertz-Versuch), durch Beschuss mit elektromagnetischer Strahlung (Schwarzlicht) oder auch Erwärmung (Glühlampe). Die zugführte Energie wird dann von einem Elektron in der Atomhülle aufgenommen. Das führt dazu, dass das Elektron auf ein höheres Energieniveau angehoben wird. Ein höheres Energieniveau heißt, dass es seinen Radius der Kreisbahn um den Atomkern erhöht. Es bewegt sich also nach der Energiezufuhr, der Anregung, weiter entfernt vom Kern als vor der Anregung. Man spricht von einem elektronischen Übergang. Kurz darauf gibt das Elektronk diese Energie wieder ab und strahlt sie zurück. Diese abgestrahlte Energie wird immer als elektromagnetische Strahlung abgegeben, oft als Licht, das wir dann sehen können. Die wissenschaftliche Beobachtung des abgestrahlten Lichtes von Körpern nennt man Spektroskopie. Das abgestrahlte Licht hat dabei eine Energiemenge E=h·f. Das kleine h ist das Planksche Wirkungsquantum (eine Konstante) und f ist die Frequenz des Lichts, die man messen kann. In dem klassischen Modell von Atomhüllen kann man einem Elektron jede beliebig kleine Energiemenge zuführen und es müsste dadurch angeregt werden und jeden beliebigen Energiewert E abstrahlen können. Die abgestrahlten Lichtpakete nennt man Photonen oder auch Lichtquanten. Es gibt in der klassischen Physik keinen Grund für die Annahme, dass bestimmte Energiemengen zu einer Anregung führen, andere aber nicht. Aber genau das ist der Fall. Die Spektroskopie der Atome hat eindeutig gezeigt, dass für jede Atomart immer nur ganz bestimmte Energiepakete, das heißt Energiemengen, zu einer Anregung führen und abgetrahlt werden. Jede Atomart hat ihr eigenes ganz spezifisches Muster abgestrahlter Farben. Das Spektrum abstrahlbaren Lichtes eines Atoms ist nicht kontinuierliche sondern gestückelt, gequanten oder diskret. Man spricht von einem sogenannten Linienspektrum ↗

Energiequantelung in Atomhüllen


Im vorherigen Abschnitt haben wir gesehen, dass im klassischen Planetenmodell ein Atom eigentlich so angeregt werden können müsste, dass es Licht mit jeder beliebigen Frequenz abtrahlen kann. Aber das tun sie nicht. Eine bestimmte Atomsorte strahlt nur weniger erlaubter Frequenzen und damit auch nur weniger erlaubter Energiemengen der Photonen (Lichtquanten) ab. Die abgestrahlte Energiemenge entspricht dem Energieunterschied zwischen einem angeregten Zustand eines Elektrons und seinem nicht angeregten Grundzustand. Wenn diese Unterschiede nur bestimmte Werte annehmen dürfen, dann kann man jetzt im Umkehrschluss folgern, dass auch die Energieunterschiede zwischen zwei Elektronenzuständen in der Atomhülle immer nur diese Werte annehmen können. Nimmt man zusätzlich jetzt noch an, dass es genau einen kleinstmöglichen Energiezustand eines Elektrons in einem Atom gibt, dann kommt man zu einer begrenzten Anzahl von Energiezuständen von Elektronen in Atomhüllen. Die Energie von Elektronen in der Atomhülle ist also gequantelt.

Bohrsches Atommodell


Die Befunde der Spektroskopie, der äußere photoelektrische Effekt sowie der Franck-Hertz-Versuch waren Anzeichen, die schon früh im 20ten Jahrhundert auf eine Quantelung der Energie in der Atomhülle hinwiesen. Der dänische Physiker Niels Bohr verband diese Erkenntnisse im Jahr 1913 mit den damals vorherrschenden Planetenvorstellungen [
10] der Atomhülle zu einem neuen Atommodell. Bohr stellte sich die Elektronen noch immer auf einer Art Planetenbahn vor, gab aber zumindest für das Wasserstoffatom Regeln an, welche dieser Bahnen erlaubt oder welche dieser Bahnen nicht erlaubt sind. Bohrs Atommodell ist damit das erste Atommodell, welches eine Quantelung von Energie berücksichtigt. Siehe auch Bohrsches Atommodell ↗

Franck-Hertz-Versuch


Als wichtiger Beleg für die nur gequantelte Aufnahme von Energie durch die Elektronenhülle von Atomen gilt der Franck-Hertz-Versuch von 1914: man schießt Elektronen durch ein Gas aus einzelnen Molekülen oder Atomen. Dabei stoßen manche der Elektronen mit den Gasteilchen zusammen. Man unterscheidet zwei Arten von Zusammenstoß: einen elastischen und einen inelastischen Stoß. Beim elastischen Stoß bleibt die Gesamtmenge an kinetischer Energie von Gasteilchen und Elektronen vor und nach dem Stoß gleich groß. Es geht keine Bewegungsenergie durch Umwandlung in eine andere Form von Energie verloren. Daneben gibt es aber auch sogenannte inelastische Stöße. Bei diesen wird ein Teil der Bewegungsenergie in irgendeine andere Energieform umgewandelt. Bei einer Kollision von Elektronen mit Gasteilchen ist diese andere Energieform das Anheben von Elektronen aus der Atomhülle des Gasteilchens auf ein höherers Energieniveau. Die so verlorene kinetische Energie äußert sich in einer deutlichen Verlangsamlung der Elektronen. Der Beleg für die quantisierte Aufnahme von Energie durch die Atomhüllen kommt dadurch zustande, dass bei langsamen Elektronen nur elastische Stöße mit den Gasteilchen auftreten. Erst ab einer Mindestmenge an kinetischer Energie der abgeschossenen Elektronen übernimmt die Atomhülle der Gasteilchen etwas von der kinetischen Energie der Elektronen: die Menge an Energie muss ein Mindestmaß überschreiten, um von der Atomhülle aufgenommen werden zu können. Siehe mehr unter Franck-Hertz-Versuch ↗

Lichtenergie


Um das Jahr 1905 betrachtete man Licht als eine Schwingung von feinsten kleinsten Teilchen, dem Äther. Ähnlich wie sich eine Welle im Wasser als reine Schwingung von Wassermolekülen ausbreitet, so sollte sich auch Licht als reine Schwingung um hypothetischen Ätherstoff ausbreiten. Man sprach von der Undulations- oder Wellentheorie des Lichts. In dieser Sichtweise könnte Energie in beliebigen Mengen von Wellen transportiert werden. Die Energie von Licht wäre nicht gestückelt, nicht gequantelt.

Diese Wellen- oder Undulationstheorie des Lichts zweifelte Albert Einstein im Jahr 1905 an. Aus rein theoretischen Betrachtungen folgerte Einstein, dass Licht seine Energie gestückelt, quantenhaft, transportieren könnte. Die Menge an Energie, die ein so gedachten Lichtteilchen, ein von ihm so genanntes Photon, dann hat ist:

  • E = h·f

Das große E ist die gequantelte Energiemenge, das kleine h steht für die Planck-Konstante, auch Plancksches Wirkungsquantum genannt. Und das kleine f ist die für das Licht einer bestimmten Farbe oder Wellenlänge typische Frequenz. Die anschauliche Deutung dieser Formel besagt: für eine konstante, gegebene Frequenz f kann ein Lichtteilchen nicht jede beliebige Energie besitzen sondern immer nur ein Vielfaches des immer konstanten Wertes von h.

ZITAT:

"Es scheint mir nun in der Tat, daß die Beobachtungen über die 'schwarze Strahlung', Photoluminiszenz, die Erzeugung von Kathodenstrahlen durch ultraviolettes Licht und andere die Erzeugung bez. Verwandlung des Lichtes betreffende Erscheinungsgruppen besser verständlich erscheinen unter der Annahme, daß die Energie des Lichtes diskontinuierlich im Raume verteilt sei. Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahles die Energie nicht kontinuierlich auf größer und größer werdene Räume verteilt, sondern es besteht dieselbe aus einer endlichen Zahl von in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen und nur als Ganze absorbiert und erzeugt werden können."[8]

Bezieht man die Quantelung von Energie auf einzelne Teilchen von Licht, so kann man diese auch als Lichtquanten oder allgemeiner als Energiequanten bezeichnen. Albert Einstein beschrieb solche Energiequanten zu Erklärung des Schwarzen Strahlers und der Photoemission als eine nicht weiter teilbare Menge von Energie, die an einem Raumpunkt konzentriert (lokalisiert) ist, bei der Ausbreitung nicht teilen und nur als ganzes absorbiert oder erzeugt werden. Klassische Versuche oder Effekte, die zur Idee einer Quantelung von Licht führten waren:


Andere Quantelungen


Energie ist nicht die einzige Größe der Physik, die in der Wirklichkeit oft nur gequantelt beobachtet wird. Auch die elektrische Ladung kommt nur in einer kleinstmöglichen Menge, der Elementarladung, oder als Vielfache, also Anhäufungen der Elementarladung vor. Das zeigte zum Beispiel der berühmte Millikan-Versuch.[15] Neben der Energie sind zum Beispiel auch Bahn- und Eigendrehimpuls gequantelt. In einem etwas erweiterten Sinn wird auch spekuliert, ob Raum und Zeit in kleinsten Stücken, den sogenannten Planck-Längen oder Planck-Zeiten vorkommt, also letztendlich gequantelt wäre. Siehe mehr dazu im Artikel zur Quantelung ↗

Quantenphilosophisch


Das So-Sein der Welt


In der Zeit um 19000 stellte Max Planck zu seiner Bestürzung fest, dass elektromagnetische Strahlung einen schwarzen Strahlen möglicherweise nur quantisiert verlassen kann[1]. Bis dahin ging man davon aus, dass Strahlung alle beliebigen Energiewerte annehmen kann, in der Sprache der Physik also eine kontinuierliche Größe ist. Diese Prinzip erkannte man später auch in anderen Gebieten der Physik, zum Beispiel wie oben erklärt in den Hüllen von Atomen. Wer sich einmal einige Originalveröffentlichungen aus jener Frühzeit der Quantenphysik ansieht[2][5], erkennt darin die Verwunderung der Naturforscher über diesen Umstand. Es gibt kein tieferes, fundamentaleres Prinzip, aus dem die Quantelung von Energie notwendigerweise abgeleitet werden könnte. Die Natur scheint einfach so geschaffen zu sein, ohne dass wir ein wozu oder warum erkennen können. Die selbe faktische Gegebenheit begegnet uns auch etwa bei der Lichtgeschwindigkeit. Sie beträgt im Vakuum etwa 300 Tausend Kilometer pro Sekunde. Warum nicht zum Beispiel nur 100 km/h oder eine Millionen km/s? Wir wissen es nicht. In der Philosophie der Physik spricht man hier von einer sogenannten Kontingenz oder auch dem So-Sein der Welt ↗

Realität als Simulation


Verschiedene Autoren spielten die Idee durch, dass die physikalische Realität, so wie wir sie wahrnehmen, das Ergebnis einer Art Computerberechnung sein könnten.[6][7] Die Quantelung in der Physik wäre dann möglicherweise Ausdruck einer Simulation der Welt als diskretes Modell, etwa wie die Finiten Elemente in der Materialwissenschaft, Zellularautomaten der Informatik oder Konrad Zuses rechnender Raum. Die Analogie zur Quantelung wird dann zum Beispiel in der Metapher von Pixeln auf einem Bildschirm beschrieben. Wenn man die Formel s=½at² für den freien Fall eines Körpers in Richtung Oberfläche eines Himmelsköpers nimmt, kann man für die Falldauer t beliebig fein gestückelte Zeiten einesetzen. Mit reellen Zahlen als Definitionsmenge (x-Werte) und als Wertevorrat (y-Menge) sind für beliebig fein aufteilte Zeiten auch beliebig fein unterscheidbare Positionen als y-Werte möglich. Sagt man jetzt aber, dass der y-Wert auf einem Bildschirm mit Pixeln die momentane Höhe eines Punktes über dem Boden angeben soll, dass bilden die am Bildschirm umsetzbaren y-Werte der Pixel kein Kontinuum mehr. Als Pixelkoordinate sind üblicherweise nur ganze Zahlen erlaubt. In dieser Analogie könnten dann die zugrundeliegenden Formeln zur Berechnung von Veränderungen in der Welt zwar kontinuierlich sein, aber die Realisierung der berechneten Werte in der beobachtbaren Wirklichkeit für dazu, dass sie in diskrete Werte überführt werden müssen. Und genau das ist eine zentrale Beschaffenheit der Quantenphysik: die Formeln für die Veränderung der Wahrscheinlichkeiten für Messgrößen ist kontinuierlich, die gemessenen Größen in der Realität aber diskret. Diese Analogie ist eine Motivation für die sogenannte Simulationshypothese ↗

Quantelung und Quantisierung


Die beiden Worte Quantelung und Quantisierung beziehen sich beide auf denselben Sachverhalt, bezeichnen aber unterschiedliche Aspekte davon. Während die Quantelung die tatsächliche Stückelung von Dingen in kleinstmögliche Pakete meint, versteht man unter einer Quantisierung eher die (mathematische) Modellierung von gequantelten Zuständen oder deren Änderungen. Die Quantisierung erkennt man in Formeln oft an einem kleinen n, das dann für natürliche Zahlen (einschließlich der Null) steht. Damit kann für das n zum Beispiel die 1 oder auch die 2 als Wert eingesetzt werden, nicht aber die 1,1 oder die 1,99995. Siehe mehr unter Quantisierung ↗

Fußnoten


  • [1] Über eine Verbesserung der Wienschen Spektralgleichung. In: Verhandl. Dtsch. Phys. Ges. Band 2, 1900, S. 202–204.
  • [2] Albert Einstein: Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. In: Annalen der Physik. Band 322 (Band 17 der 4. Folge), 1905, S. 132–148. doi: http://dx.doi.org/10.1002/andp.19053220607
  • [3] Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum. In: Verhandl. Dtsch. Phys. Ges. Band 2, 1900, S. 237–245.
  • [4] Über das Gesetz der Energieverteilung im Normalspektrum. In: Ann. Phys. Band 4, Nr. 3, 1901, S. 553–563, doi:10.1002/andp.19013090310
  • [6] Konrad Zuse: Rechnender Raum. Braunschweig: Friedrich Vieweg & Sohn. 1969. 70 Seiten.
  • [7] Stephen Wolfram, A New Kind of Science. (Wolfram Media, 2002). 1197 Seiten.
  • [8] Energiequanten nach Albert Einstein, 1905: "Es scheint mir nun in der Tat, daß die Beobachtungen über die 'schwarze Strahlung', Photoluminiszenz, die Erzeugung von Kathodenstrahlen durch ultraviolettes Licht und andere die Erzeugung bez. Verwandlung des Lichtes betreffende Erscheinungsgruppen besser verständlich erscheinen unter der Annahme, daß die Energie des Lichtes diskontinuierlich im Raume verteilt sei. Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahles die Energie nicht kontinuierlich auf größer und größer werdende Räume verteilt, sondern es besteht dieselbe aus einer endlichen Zahl von in Raumpunkten lokalisierten Energiequanten, welche sich bewegen, ohne sich zu teilen und nur als Ganze absorbiert und erzeugt werden können." In: Annalen der Physik. Band 322, Nr. 6, 1905, S. 132–148, doi:10.1002/andp.19053220607. Dort die Seite 133. Siehe mehr unter Energiequant ↗
  • [9] Der Physiker und Nobelpreisträger Richard Feynman (1918 bis 1988) machte deutlich, dass jedes Planetenmodell des Atoms heute als überholt gilt: "In der ersten Zeit nach der Entdeckung der Elektronen betrachte man die Atome als eine Art kleiner Sonnensysteme, bestehend aus einem schweren Zentrum (dem Atomkern) und Elektronen, die es, ähnlich wie die Planeten die Sonne auf bestimmten 'Bahnen' umkreisen. Wer sich diese Atomvorstellung bewahrt hat, lebt, was die Entwicklung der Physik betrifft, im Jahre 1910." In: Richard Feynman: QED: Die seltsame Theorie des Lichts und der Materie. Piper Verlag. 1. Auflage 1992. ISBN: 3-492-21562-9. Dort die Seiten 99 und 100. Siehe auch saturnisches Atommodell [Planetenmodell] ↗
  • [10] Die Vorstellung eines Atoms in Form eines Miniatur-Sonnensystems, mit den Elektronen auf Kreisbahnen in einer gemeinsamen Ebene, gilt heute als überholt. Ein entsprechendes Atommodell nennt man heute planetarisches Atommodell oder auch saturnisches Atommodell ↗
  • [12] Wilhelm Ludwig Franz Hallwachs (1859 bis 1922): Ueber die Electrisierung von Metallplatten durch Bestrahlung mit electr. Licht. In: Annalen der Physik, Bd. 270 (Wiedemann's Annalen. 34) 1888, S. 731–734. Auch in: Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1888. Dort die Seiten 174 bis 176. Siehe auch Hallwachs-Versuch ↗
  • [14] Der Begriff Lichtquant wurde im Jahr 1905 geprägt von Albert Einstein und parallel zu dem Wort Energiequante mehrfach wörtlich verwendet in: Albert Einstein Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. In: Annalen der Physik. Band 322, Nr. 6, 1905, S. 133. Siehe auch Lichtquant ↗
  • [15] Millikan zeigte in einem sehr aufwändigen und diffizilen Experiment, dass die Ladungsmengen alle auf kleinsten Öltröpfchen alle einen größten gemeinsamen Teiler haben. Dieser größte gemeinsame Teiler war dann die Elementarladung. Siehe auch Millikan-Versuch ↗
  • [16] Zunächst ging Boltzmann davon aus, dass jedes Teilchen im Gas kontinuierlich unendlich viele Zwischenzustände zwischen zwei verschiedenen kinetischen Energien (lebendige Kraft) einnehmen könnte: "Die lebendigen Kräfte gehen continuirlich in einander über". Doch mathmatisch ist das sehr schwer handhabbar, daher modellierte er die kinetische Energie der Gasteilchen zunächst diskret: "Wir wollen zunächst annehmen, jedes Molekül sei nur im Stande, eine bestimmte endliche Anzahl von Geschwindigkeiten anzunehmen". In: Ludwig Boltzmann: Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. In: Sitzungsber. d. k. Akad. der Wissenschaften zu Wien II 76, S. 428 (1877). Nachdruck in Wissenschaftliche Abhandlungen von Ludwig Boltzmann, Band II., S. 164–223. Siehe auch Kontinuum ↗
  • [17] Dass die kinetische Energie der Gasteilchen vielleicht doch auch real in der Wirklichkeit in abzählbaren kleinsten Energieatomen vorkommen könnte, vermutete Ludwig Boltzmann spätestens im Jahr 1891 der Physiker. Zum Abzählproblem der Entropie über die Idee der Mikrozustände im Verhältnis zu bestimmten Makrozuständen heißt es, Boltzmann, "brauchte […] die diskreten Energieniveaus, um die Zahl der Zustände abzhälen zu können." Dabei habe er die "diskreten Energieniveaus" aber nicht nur als "mathematischen Kunstgriff" betrachtet. Boltzmanns Kollege Ostwald habe in seiner Autobiographie "Lebenslinien" festgehalten, dass Boltzmann im Jahr 1891 in einer "Naturforscherversammlung" in Halle an der Saale in einem Gespräch eingworfen: "Ich sehe keinen Grund, nicht auch die Energie als atomistisch eingeteilt zu sehen." In: Karl von Meyënn: Die Grossen Physiker. Band I: Von Aristoteles bis Kelvin. Band II: Von Maxwell bis Gell-Mann. C. H. Becksche Verlagsbuchhandlung. München. 1997. ISBN für beide Bände: 3 406 41151 7. Dort im Kapitel Ludwig Boltzmann, verfasst von Dieter Flamm. Seite 65. Siehe auch Entropie ↗