ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Franck-Hertz-Versuch

Physik

© 2016 - 2025


Basiswissen｜ Ideengeschichtlicher Hintergrund｜ Grundgedanke des Franck-Hertz-Versuches｜ Aufbau des Franck-Hertz-Versuches｜ Zweck des Aufbaus｜ Durchführung des Franck-Hertz-Versuches｜ Beobachtung am Franck-Hertz-Versuch｜ Deutung: Es kommt zu einer Stoßionisation｜ Deutung: elastische und inelastische Stöße｜ Ideale und reale Gase｜ Typische Daten mit Quecksilberatomen [4]｜ Typische Daten mit Neonatomen｜ Zusammenfassende Kernaussage des Versuchs｜ Gäbe es eine Alterantive Deutung?｜ Original-Literatur


Basiswissen


Energiequantelung in der Elektronenhülle: der Franck-Hertz-Versuch wurde erstmals in den Jahren 1911 bis 1914 von James Franck[5] und Gustav Hertz[6] durchgeführt und stützte den Gedanken diskreter (gequantelter) Energieniveaus in Atomen. Dieser Befund stärkte damit das damals noch junge Bohrsche Atommodell[14], wennauch Franck und Hertz in ihrer Veröffentlichtung aus dem Jahr 1914 das Bohrsche Atommodell noch nicht erwähnten, Bohr aber die Quantelung voraussagte.[23]



Bildbeschreibung und Urheberrecht
Die klassische Kurve mit dem hügelartigen Anstieg, hier in Anlehnung an den Originalversuch von 1914. © Ahellwig (Wikimedia) ☛


Ideengeschichtlicher Hintergrund


Franck und Hertz führten den Versuchen in der Zeit um 1914 durch. Zu dieser Zeit stellte man sich den inneren Aufbau der Atome ähnlich einem kleinen Sonnensystem vor.[16] Ernest Rutherford hatte im Jahr 1911 gezeigt, dass die Elektronen um einen inneren schweren Kern angeordnet sind.[17] Eine wichtige Quelle von Informationen zu den Atomen war die Analyse des von Atomen absorbierten und emittierten Lichts, die sogenannte Spektroskopie.[18]. Dabei hatte man festgestellt, dass Atome einer bestimmten Art, etwa Quecksilber, Licht immer nur in eng definierten Bereichen einer Frequenz aufnehmen oder abgeben. Diese Frequenzen sind typisch für jede Atomart. Und Albert Einstein hatte im Jahr 1905 die Idee vorgestellt, dass Licht in Form von Energie- oder Lichtquanten existiert[19], das heißt in räumlich eng begrenzten festen Mengen an Licht. Und jedes dieser Lichtquanten hat nach der Formel E=hf eine seiner Frequenz fest zugeordnete Energiemenge.

MERKSATZ:

1.0 Die Aufnahme und Abgabe von Licht einer bestimmten Art von Atom geschieht immer nur in ganz eng definierten Frequenzbereichen. Jede Frequenz steht dabei für Lichtteilchen einer bestimmtem Menge an Energie.

Die empirischen Beobachtungen der Spektroskopie in Verbindung mit Einsteins Idee von Lichtquanten legte es also nah, dass Atome in ihrem Inneren Energie nur in festen Paketen, den Energiequanten aufnehmen oder abgeben konnten. Und genau das war auch der Kerngedanke des Bohrschen Atommodells.[14] Das nun auch durch einen Versuch bestätigt zu haben, war die Leistung von Franck und Hertz.

Grundgedanke des Franck-Hertz-Versuches


Gasatome können Energie aufnehmen und damit ihre eigene Geschwindigkeit verändern. Die aufgenommene Energie liegt dann in Form von kinetischer Energie (Bewegung) vor. Gasatome können Energie aber auch aufnehmen, um in einen angeregten Zustand überzugehen: Elektronen in ihren Schalen wechseln dabei auf ein höheres Energieniveau. Man spricht von einem sogenannten elektronischen Übergang oder einer Anregung des Atoms. Die mit einem solchen Übergang umgesetzte Energie verändert nicht die Geschwindigkeit des betroffenen Gasatoms.

MERKSATZ:

2.0 In den Worten von Franck und Hertz: "Die neue Methode der Messung der Ionisierungsspannung beruht darauf, dass die Ionisierungsarbeit der größte Wert ist, den die kinetische Energie der Elektronen besitzen darf, damit diese noch bei einer größeren Zahl von Stößen ohne Energieverlust von den Gasmolekülen reflektiert werden."

Mit dem Franck-Hertz-Versuch wurden zwei Dinge gezeigt: a) Man kann Gasatome durch Zusammenstöße mit Elektronen anregen (Elektronen-Sprung). b) Werden sie angeregt, geschieht dies nicht fließend mit beliebig klein veränderbaren Energiemengen sondern immer nur in Energiepaketen konstanter Größe. Die Anregung erfolgt gequantelt. Dieser Befund war zur Zeit des Experiments nicht selbstverständlich.

Aufbau des Franck-Hertz-Versuches


In einem horizontal liegenden Glaskolben befindet sich ein dünnes Gas. Üblich sind Quecksilberdampf oder Neon bei etwa 10 bis 20 Millibar (10 bis 20 tausendstel bar). An einer Seite, meist links dargestellt, befindet sich eine Metallplatte, die Glühkathode K. Richtung Mitte des Kolbens, einige Zentimeter von der Glühkathode entfernt, befindet sich ein Gitter G. Es hat gegenüber der Kathode K ein positives Potential von einigen wenigen Volt. Am Ende gegenüber der Glühkathode K, direkt hinter dem Gitter, liegt eine weitere Metallplatte, die Auffanganode A. Sie hat ein leicht negatives Potential gegenüber dem Gitter K von vielleicht etwa einem Volt.[22]

Zweck des Aufbaus


  • Durch Erhitzung der Glühkathode treten aus dieser dann freie Elektronen aus.
  • Diese werden von dem positiven Potential des Gitters G angezogen.
  • Auf dem Weg zwischen Kathode K und Gitter G sollen sie mit Gasatomen zusammenstoßen.
  • Letzendlich erreichen Sie das Gitter K. Manche werden vom Gitter geschluckt.
  • Manche Elektronen durchfliegen das Gitter und fliegen dann weiter Richtung Anode A.
  • Da das Gitter G aber stärker positiv ist als die Anode A, werden sie Richtung Gitter gezogen.
  • Manche Elektronen landen deshalb am Ende doch wieder auf dem Gitter, andere erreichen die Anode A.
  • Die Elektronen, die die Anode A erreichen, können als sehr kleiner Stromfluß mit einem Amperemeter[15] gemessen werden.
  • Die Höhe des Potentialunterschiedes (Spannung U) zwischen Gitterplatte G und Anode A ist regelbar.

Durchführung des Franck-Hertz-Versuches


  • Die Kathode K wird aufgeheizt, dadurch treten langsame Elektronen aus ihr aus.
  • Zwischen der Kathode K und dem Lochgitter G wird die sogenannte Beschleunigungsspannung Ub eingestellt.
  • Die Kathode K ist dabei negativ gegenüber dem Gitter G. Die Kathode stößt die Elektroden ab, das Gitter zieht sie an.
  • Gleichzeitig liegt eine Gegenpannung Ug zwischen dem Gitter G und der Auffanganode A an. Sie bremst Elektronen ab.
  • Für den Versuch wird nun die Beschleunigungsspannung langsam erhöht.
  • Man beobachtet dann den Stromfluß (Elektronfluß) an der Anode A.

Beobachtung am Franck-Hertz-Versuch



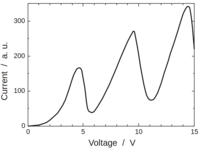
Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.
Der klassische Kurvenverlauf für den Franck-Hertz-Versuch: eine sägezahnartig ansteigende Linie

  • Überschreitet die Beschleunigungsspanung Ub den Betrag der Gegenspannung Ug wird erstmals ein Stromfluß an A gemessen.
  • Dieser Strom steigt dann weiter an, wenn die Beschleunigungsspanung weiter erhöht wird.[7]
  • Ab einem bestimmten Spannungswert fällt er dann plötzlich ab auf einen deutlich kleineren Wert.[8]
  • Erhöht man dann die Beschleunigungsspannung Ub weiter, steigt der Anodenstrom wieder an.[9]
  • Ab einer bestimmten Beschleunigungsspannung fällt er dann wieder steil ab.
  • Der Abfall ist nicht ganz so tief wie beim ersten Mal aber immer noch deutlich.
  • Dieser zweite Spannungsabfall passiert etwa 4,9 Volt über dem ersten Spannungsabfall.
  • Erhöht man die Spannung weiter, wird sich dieses Verhalten in guter Näherung fortsetzen:
  • Immer, wenn man die Beschleunigungsspanung um etwa 4,9 Volt erhöht, fällt der Anodenstrom deutlich ab.

Deutung: Es kommt zu einer Stoßionisation


Neben der Bestätigung, dass die Energiezustände in Atomen als Ganzem auch der Quantelung der Energie unterliegen, zeigte der Versuch darüberhinaus noch, dass Atome durch Stöße von zum Beispiel Elektronen angeregt werden können. Vorher dachte man, dass das möglicherweise nur durch Lichtquanten geschehen könne. Man spricht von einer Stoßionisation ↗

Deutung: elastische und inelastische Stöße


Von Quecksilberatomen weiß man, dass sie für eine Anregung in den ersten Anregungszustand eine Energie von mindestens 4,9 Elektronenvolt (eV) benötigen. Beschießt man solche Atome nun mit Elektronen, deren kinetische Energie (pro Elektron) weniger als 4,9 eV beträgt, dann kann kein Quecksilberatom diese kinetische Energie in sich aufnehmen, das heißt: nicht angeregt werden. Die Energie eines Elektrons kann sich dann nach den Gesetzen eines vollkommen elastischen Stoßes nur als kinetische Energie zwischen den beteiligten Elektronen und Atomen verteilen. Kein Quecksilberatom kann also angeregt werden und nach der Anregung zum Beispiel Lichtquanten aussenden. Beträgt die Energie der einzelnen Elektronen aber mehr als 4,9 eV, dann kann bei einem Stoß ein Teil der Energie in das Quecksilberatom hineingehen und es anregen: ein Elektron im Atom wechselt auf eine höhere Bahn. Der Stoß ist nun teilweise inelastisch, das heißt, der Stoß nimmt Energie auf, die als kinetische Energie verloren geht. Das Quecksilberatom wird angeregt und geht kurz darauf wieder in den Grundzustand zurück. Dabei sendet er ein Lichtquant (Photon) aus. Die Frequenz des ausgesandten Quants liegt bei 1,18 mal 10 hoch 15 Hertz.

Ideale und reale Gase


In der sogenannten kinetischen Gastheorie betrachtet man Gasteilchen als kleine Kügelchen, die sich bei einer Kollision vollkommen elastisch verhalten. Elastisch heißt, dass sie vor und nach der Kollision zusammengenommen dieselbe kinetische Energie haben wie vor dem Stoß. Die kinetische Energie wird damit nicht umgewandelt in zum Beispiel Verformungsenergie oder Wärme. Bei der Anregung eines Atoms bei einer Kollision gilt das nicht mehr: ein Teil der kinetischen Energie der Stoßpartner wird in Anregungsenergie umgewandelt und geht damit als kinetische Energie verloren[3, Seite 229]. Ein solches Gas ist dann auch nicht mehr ideal sondern ein reales Gas ↗

[4]">

Typische Daten mit Quecksilberatomen[4]


  • In der Glasröhre befinden sich als Gas Quecksilberatome.
  • Bei einer Beschleunigungsspannung von 4,9 Volt fällt die Stromstärke erstmals steil ab.
  • 4,9 Elektronenvolt ist die Anregungsenergie für die Quecksilberatome.[10]
  • Das Elektron fällt ohne Zwischenstufen auf sein Anfangsniveau zurück.
  • Bei jedem natürlichzahligen Vielfachen von 4,9 Volt wiederholt sich der Spannungsabfall
  • Die Frequenz der abgestrahlen Photonen liegt bei 1,18 mal 10 hoch 15 Hertz.

Typische Daten mit Neonatomen


  • In der Glasröhre befinden sich Neonatome.
  • Bei einer Beschleunigungsspannung von 18,4 Volt fällt die Stromstärke erstmals steil ab.
  • 18,4 Elektronenvolt ist die Anregungsenergie für die Neonatome.
  • Das Elektron fällt mit Zwischenstufen auf sein Anfangsniveau zurück.
  • Die erste Zwischenstufe liegt 2,5 Elektronenvolt tiefer.
  • Das entsprechend ausgesandte Quant ist sichtbar.
  • Es erscheint uns als orange bis gelbes Licht.

Zusammenfassende Kernaussage des Versuchs


Franck und Hertz deuten die Ergebnisse ihres Versuches als eine Bestätigung der damals, 1914, noch jungen "Quantentheorie". Aus der Analyse der sogenannten Spektrallinien hatte man festgestellt, dass Atome einer bestimmten Art stets Licht in charakteristischen Farben, das heißt auch charakteristischer Frequenzen aussendet. Die Energie des ausgesandten Lichts entsprach dabei der Änderung der Energie des Atoms. Diese Änderungen waren nicht fließen kontinuierlich sondern erfolgten in Paketen, den Quanten. Franck und Hertz fassten ihre Befunde mit den folgenden Worten zusammen:

  • 1. Es wird gezeigt, daß die Elektronen im Quecksilberdampf elastische ZusammenstoBe mit den Molekulen erleiden bis zu einer kritischen Geschwindigkeit.
  • 2. Es wird ein Verfahren beschrieben, diese kritische Geschwindigkeit auf ein Zehntel Volt genau zu messen. Sie ist gleich der Geschwindigkeit, diee
Elektronen besitzen, die 4,9 Volt durchlaufen haben.
  • 3. Es wird gezeigt, daß die Energie eines 4,9-Voltstrahles genau gleich einem Energiequantum der Quecksilberresonanzlinie 253,6 pm ist.
  • 4. Es werden die Grunde dafur diskutiert, daß bei der Energieabgabe der 4,9-Voltstrahlen an die Quecksilbermolekule ein Teil der Stöße zur Ionisation fuhrt, so daß 4,9 Volt die Ionisierungsspannung des Quecksilberdampfes wäre. Ein anderer Teil der Stöße scheint Lichterregung hervorzurufen, von
der wir vermuten, daß sie in der Emission der Linie 253,6 pm besteht.

Soweit das Zitat.[1, am Ende] Die von Franck und Hertz festgehaltenen Ergebnisse bedeuten: nur wenn die Energie, die einen Atom zugeführt wird, mindestens so groß ist wie dieses Quant, kann das Atom die Energie aufnehmen. Die Größe dieser Energie, so die Theorie, entspricht dabei der Frequenz des Lichts ν[11] multipliziert mit der Planck-Konstanten h. Die Formel ist E=hν[12]. Genau diesen Zusammenhang mit der Theorie zeigten die Versuchsergebnisse von Franck und Hertz. Man spricht auch von einer "quantenhaften Energieabsorption"[20] oder von "quantisierten Energien im Atom".[21] Siehe auch Energiequantelung ↗

Gäbe es eine Alterantive Deutung?


Man beobachtet, dass die Elektronen ab einer bestimmten Geschwindigkeit ihre Energie abgeben. Eine Möglichkeit ist, dass sie ihre Energie als Ionisierungsenergie an die Quecksilberatome übertragen. Eine zweite Möglichkeit ist, dass die Elektronen ihre Bewegungsenergie ab einem gewissen Schwellenwert ohne Ionisierung in Lichtenergie umwandeln. Diese Möglichkeit wurde von Franck und Hertz diskutiert, ohne dass der oben beschriebene Befund dabei in Frage gestellt werden muss.[13]

Original-Literatur


  • [3] Richard T. Weidner; Robert Sells: Elementare moderne Physik. Verlag Friedrich Vieweg & Sohn, Ausgabe von 1982. ISBN: 3-528-8415-4. Siehe auch Elementare moderne Physik ↗
  • [4] Oskar Höfling: Physik. Lehrbuch für Unterricht und Selbststudium. Fünfzehnte Auflage. 1994. ISBN: 3-427-41045-5. Siehe auch der Höfling ↗
  • [5] James Franck (1882 bis 1964) war ein deutsch-amerikanischer Physiker. Im ersten Weltkrieg arbeitete er zusammen mit Fritz haber an Gaswaffen. Zwischen den zwei Kriegen wirkte er vor allem in Göttingen, zusammen mit Max Born. 1934 bat er die Universität Göttingen aufgrund des Antisemitismus in Deutschland um seine Entlassung und wanderte dann in die USA aus. Dort forschte er unter anderem über die Photosynthese. Siehe auch James Franck ↗
  • [6] Gustav Hertz (1887 bis 1975) war ein deutscher Physiker. Nach dem zweiten Weltkrieg arbeitete er am sowjetischen Atomprogramm mit, später wirkte er in der ehemaligen DDR. Siehe auch Gustav Hertz ↗
  • [7] In der original-Veröffentlichung aus dem Jahr 1914: "Es zeigte sich dabei, daß die Elektronen an den Quecksilberatomen ohne Energieverlust reflektiert werden, solange ihre Geschwindigkeit einer durchlaufenden Spannung von weniger als 5 Volt entspricht." In: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/phbl.19670230702
  • [8] In der original-Veröffentlichung aus dem Jahr 1914: "Schon aus diesen Messungen erkennt man, daß der plötzliche Eintritt der unelastischen Stöße im Quecksilberdampf dann eintritt, wenn die Strahlen etwa 5 Volt durchlaufen haben, d. h. etwa 5 Volt würde die Ionisierungsspannung des Quecksilberdampfes sein." In: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/phbl.19670230702
  • [9] In der original-Veröffentlichung aus dem Jahr 1914: " Solange die beschleunigende Spannung kleiner ist als die verzögernde, ist der Strom Null. Dann wird er ansteigen, bis die beschleunigende Spannung gleich der Ionisierungsspannung geworden ist. In diesem Augenblick werden die Elektronen in der Nähe des Drahtnetzes unelastische StoBe erleiden und dabei ionisieren. Da sie selbst und die bei der Ionisation befreiten Elektronen bis zum Durchtritt durch das Drahtnetz nur noch eine sehr geringe Spannung durchlaufen, so treten sie ohne merkliche Geschwindigkeit durch das Drahtnetz hindurch und sind nicht imstande, gegen das verzögernde Feld anzulaufen. Der Galvanometerstrom wird daher auf Null abfallen, sobald die beschleunigende Spannung größer geworden ist als die Ionisierungsspannung. Steigert man die beschleunigende Spannung weiter, so rückt die Stelle, an der die Elektronen unelastische Stöße erleiden, vom Drahtnetz nach innen. Die nach dem unelastischen Zusammenstoß vorhandenen Elektronen durchlaufen also auf dem Wege zum Drahtnetz eine Spannung, welche gleich der Differenz der beschleunigenden Spannung und der Ionisierungsspannung ist. Sobald diese Differenz größer geworden ist als die konstante verzögernde Spannung zwischen N und G, konnen wieder Elektronen gegen das verzogernde Feld anlaufen, und der Galvanometerstrom steigt wieder an. Da die Zahl der Elektronen durch die Ionisation vergrößert ist, steigt er noch höher an als das erste Mal. Sobald jedoch die beschleunigende Spannung gleich der doppelten Ionisierungsspannung geworden ist, erleiden die Elektronen in der Nahe des Drahtnetzes zum zweitenmal unelastische Zusammenstöße." In: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/phbl.19670230702
  • [10] "Die Werte fur den Abstand zweier benachbarter Maxima liegen samtlich zwischen 4,8 und 5,O Volt, so daß wir 4,9 Volt als den
richtigsten Wert für die Ionisierungsspannung des Quecksilberdampfes ansehen können." In: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/phbl.19670230702
  • [11] Das ν ist das kleine griechische Ny. Dieser dem lateinischen v ähnliche Buchstabe steht in der Physik für die Frequenz bei elektromagnetischen Wellen. Siehe auch kleines Ny ↗
  • [12] Franck und Hertz vergleichen ihre empirischen Werte mit den theoretisch berechneten Werten eines R. W. Wood aus dem Jahr 1914: "Beim Quecksilberdampf liegt es nahe, an die äußerst ausgesprochene Eigenfrequenz der von Wood gefundenen sogenannten Resonanzlinie des Quecksilberdampfes λ = 253,6 µm zu denken. Rechnet man das Produkt hν für diese Frequenz aus, so erhält man die Energie, die ein Elektron besitzt, das 4,84 Volt durchlaufen hat. Das ist eine so gute Übereinstimmung mit dem von uns erhaltenen Wert, daß man wohl kaum an einen Zufall glauben kann." In: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Siehe auch E=hv ↗
  • [13] Eine alternative Deutung: "In der Tat ist es durchaus möglich, die Resultate durch die Annahme zu deuten, daß das stolze Elektron seine Energie in Lichtstrahlung der Wellenlänge 253,6 µm umsetzt, sobald seine Energie den entsprechenden Betrag hv erreicht hat, ohne daß dabei eine Ionisation
auftreten müßte." Diese Möglichkeit wird ausführlich diskutiert in: James Franck, Gustav Hertz: Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. In: Verh. Dtsch. Phys. Ges. Band 16, 1914, S. 457–467, doi:10.1002/phbl.19670230702. Online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/phbl.19670230702
  • [14] Niels Bohr hatte sein Atommodell im Jahr zuvor, 1913 veröffentlicht: On the Constitution of Atoms and Molecules, Part I. In: Philosophical Magazine. 26, 1913, S. 1–25. Siehe auch Bohrsches Atommodell ↗
  • [15] In der original-Veröffentlichung wird das Amperemeter dem damaligen Sprachgebrauch folgend bezeichnet als Galvanometer ↗
  • [16] Die Idee, dass die Elektronen den Kern des Atoms ähnlich umkreisen wie die Planeten die Sonne, und sich dabei alle in einer Ebene bewegen, bezeichnet man auch als saturnisches Atommodell ↗
  • [17] Ernest Rutherford: The Scattering of the α and β Rays and the Structure of the Atom. In: From the Proceedings of the Manchester Literary and Philosophical Society, IV, 55, pp. 18-20. Siehe auch Rutherfordscher Streuversuch ↗
  • [18] Mit den Methoden der Spektroskopie hatte man festgestellt, dass bestimmte Atome Licht in immer nur sehr eng definierten Frequenzbereichen aufnimmt oder abgibt. Siehe auch Spektroskopie ↗
  • [19] Albert Einstein verwendete die Worte "Energiequant" und "Lichtquant" nebeneinander bereits im Jahr 1905. In: Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. In: Annalen der Physik. Band 322, Nr. 6, 1905, S. 133. Siehe auch Energiequant ↗
  • [20] Dorn.Bader. Physik SII Gesamtband Gymnasium. Westermann Bildungsmedien. Braunschweig. 2023. ISBN: 978-3-14-152376-8. Die "quantenhafte Energiebsorption" im Zusammenhang mit dem Frack-Hertz-Versuch wird behandelt auf den Seiten 418 und 419.
  • [21] Metzler Physik. 5. Auflage. 592 Seiten. Westermann Verlag. 2022. ISBN: 978-3-14-100100-6. Unter dem Stichwort "Quantisierte Energien im Atom" heißt es zur Bedeutung des Franck-Hertz-Versuchs: "Dies bestätigt die Hypothese, dass im Atom nur bestimmte Werte der Energie möglich sind." (Seite 349). Siehe auch Franck-Hertz-Versuch ↗
  • [22] Der hier beschriebene Aufbau des Versuchs entspricht der üblichen Darstellung in Lehrbüchern über 100 Jahre nach der Erstveröffentlichung. In ihrer Veröffentlichung aus dem Jahr 1914 wird ein etwas anderer Aufbau beschrieben, was aber nichts wesentlich an den betrachteten Phänomen ändert.
  • [23] Dass freie Elektronen ihre Energie an gebundene Elektronen in Atomen nur paketweise abgeben, sagte schon Niels Bohr 1913 aus Folgerung aus seinem Atommodell voraus: "Experiments on the phenomena of X-rays suggest that not only the emission and absorption of radiation cannot be treated by the help of the ordinary electrodynamics, but not even the result of a collision between two electrons of which the one is bound in an atom. This is perhaps most clearly shown by some very instructive calculations on the energy of β-particles emitted from radioactive substances recently published by Rutherford. These calculations strongly suggest that an electron of great velocity in passing through an atom and colliding with the electrons bound will loose energy in distinct finite quanta. As is immediately seen, this is very different from what we might expect if the result of the collisions was governed by the usual mechanical laws. The failure of the classical mechanics in such a problem might also be expected beforehand from tile absence of anything like equipartition of kinetic energy between free electrons and electrons bound in atoms." Und: "two colliding electrons, bound or free, will, after the collision as well as before, be in mechanical states. Obviously, the introduction of such an assmnption would not make any alteration necessary in the classical treatment of a collision between two free particles. But, considering a collision between a free and a bound electron, it would follow that the bound electron by the collision could not acquire a less amount of energy than the difference in energy corresponding to successive stationary states, and consequently that the free electron which collides with it could not lose a less amount." In: Niels Bohr: On the Constitution of Atoms and Molecules, Part I. Philosophical Magazine. 26, 1913, S. 1–25. Dort auf Seite 15. Philosophical Magazine. 26, 1913, S. 1–25. Dort auf Seite 19. Siehe auch Bohrsches Atommodell ↗