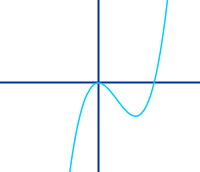
Parabel dritter Ordnung
Graph einer kubischen Funktion
© 2016
- 2026
Basiswissen|
Eigenschaften von Parabel dritter Ordnung|
Beispiele für Parabeln dritter Ordnung|
Typische Rechnungen|
Was heißt Parabel allgemein?
Basiswissen
Der Graph einer kubischen Funktion, auch ganzrationale Funktion dritten Grades, heißt Parabel dritter Ordnung. Beispiel: Die allgemeine Funktionsgleichung ist f(x)=ax³+bx²+cx+d.
Eigenschaften von Parabel dritter Ordnung
- Hat höchstens drei 👉 Nullstelle[n]
- Hat höchstens zwei 👉 Extrempunkte
- Hat höchstens eine 👉 Wendestelle
Beispiele für Parabeln dritter Ordnung
- Allgemeine 👉 f(x)=ax³+bx²+cx+d
- Sonderfall 👉 f(x)=x³-x²
- Sonderfall 👉 f(x)=x³
Typische Rechnungen
Im Zusammenhang mit einer Parabel sechster Ordnung gibt es einige Standardrechnungen, die oft durchgeführt werden, um mit wenig Aufwand einen guten Eindruck vom Verlauf des Graphen zu erhalten:
Um mit eher wenig Rechenaufwand schnell einen guten Überblick über den Verlauf einer Funktion zu erhalten bezeichnet man in der Mathematik als Kurvendiskussion. Für weitere solche Rechenarten im Bezug auf den Graphen siehe auch den Artikel zur 👉 Kurvendiskussion
Was heißt Parabel allgemein?
Das Wort Parabel bezeichnet immer ein kurvige Linie ohne gerade Teilstücke, ohne Ecken und ohne Lücken. In der Geometrie ist eine Parabel die Schnittlinie, die beim Schnitt einer (besonders ausgewählten) Ebene mit einem geraden Kegel entsteht. In der Technik steht die Parabel oft für die Flugbahn eines nicht angetriebenen Körpers (etwa eines Balles). In der Analysis ist die Parabel der Graph einer ganzrationalen Funktion ab dem Grad 2, spezielle einer quadratischen Funktion. Siehe mehr dazu im Artikel zur 👉 Parabel