Parabel vierter Ordnung
Von x-hoch-vier-Funktion
Basiswissen
Der Graph einer ganzationalen Funktion vierten Grades, auch quartische Funktion genannt heißt Parabel vierter Ordnung. Der Graph kann wie ein normale (quadratische) Parabel aussehen aber auch stark davon abweichen. Hier werden einige Grundformen kurz vorgestellt.
Beispiele
- Beispiel 1: f(x) = x^4-x^2
- Beispiel 2: f(x) = x^4+x^2
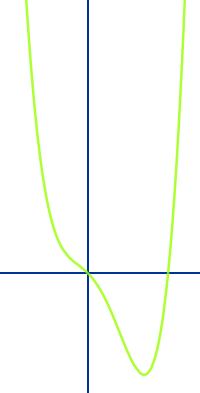
- Beispiel 3: f(x) = x^4+x^3
- Beispiel 4: f(x) = x^4+x^3+x^2
Aussehen
- Man kann die Grundformen unterscheiden:
- die => Schiefe Schüsselparabel
- die => Pseudonormalparabel
- die => Backenzahnkurve
Eigenschaften
- Kann keine eine, zwei, drei oder vier Nullstellen haben.
- Hat höchstens drei Extrempunkte.
- Hat höchsten zwei Wendestellen.
- Kann nach oben geöffnet sein.
- Kann nach unten geöffnet sein.
Synonyme
=> Parabel vierter Ordnung
=> quartische Parabel
