Basiswissen

Extrempunkte sind per Definition nur: Hochpunkte und Tiefpunkte. Hier werden kurz verschiedene Arten (lokal, relative, global, absolut) vorgestellt.

Bildbeschreibung und Urheberrecht — Hoch- und Tiefpunkte, und nur diese, nennt man Extrempunkte einer Funktion.☛

Definition

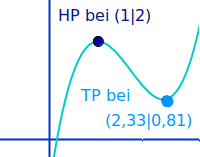
Extrempunkte sind besondere Punkte auf Funktionsgraphen. Anschaulich betrachtet sind es Gipfel von Hügeln oder die tiefsten Punkte von Tälern. Zu den Extrempunkten gehören nur Hoch- und Tiefpunkte. Als Extrempunkte gelten hier nur Punkte, für die es in ihrer Epsilon-Umgebung keine gleich hohen oder gleich tiefen anderen Punkte gibt. Das deckt sich mit der intuitiven Vorstellung, dass ein Hochpunkt höher liegen muss als seine direkten Nachbarn und ein Tiefpunkt tiefer ist als seine direkten Nachbarn. Das ist weiter erklärt unter Extrempunkt ↗

Globaler Extrempunkt

Ein globaler Extrempunkt ist dasselbe wie ein absoluter Extrempunkt.

Es ist der höchste/tiefste Punkt innerhalb des gesamten Definitionsbereiches.

Definition unter Globaler Extrempunkt ↗

Lokaler Extrempunkt

Ein lokaler Extrempunkt ist dasselbe wie ein relativer Extrempunkt.

Ihre Unmittelbaren Nachbarn sind beide kleiner oder beide größer.

Definition unter Lokaler Extrempunkt ↗

Mehrdimensionaler Extrempunkt

Dieser Begriff gehört zu mehrdimensionalen Funktion.

So nennt man Funktionen mit mehr als einer unabhängigen Variablen.

Ihre Graphen sind oft geschwungene Flächen im Raum (3D-Koordinatensystem).

Auch für solche Funktionen sind Extrempunkte definiert.

Lies unter Mehrdimensionale Extrempunkte ↗

Beispiele

Hochpunkt (-1|2) bei f(x)=x³-3x ↗

Hochpunkt (0|0) bei f(x)=-x² ↗

Tiefpunkt (1|2) bei f(x)=x³-3x ↗

Tiefpunkt (0|0) bei f(x)=x² ↗

Sonstiges

Wendepunkte sind keine Extrempunkte.

Sattelpunkte sind keine Extrempunkte.

Bestimmung

Wie man Extrempunkte mit Hilfe der ersten Ableitung f'(x) sowie anderer Methoden bestimmt, wird erklärt auf Extrempunkte bestimmen ↗