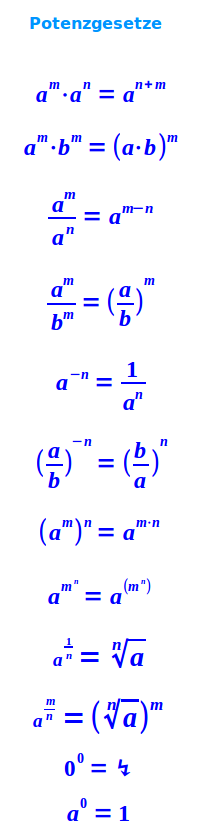Basiswissen

aᵐ·aⁿ

• Regel: aᵐ·aⁿ = aᵐ⁺ⁿ
  

• Man multipliziert zwei Potenzen mit gleicher Basis:
  

• Basis zusammenfassen, Exponenten addieren: 2³·2²=2⁵
  

• Mehr unter Potenzen mit gleicher Basis multiplizieren ↗
  

aᵐ:aⁿ

• Regel: aᵐ:aⁿ = aᵐ⁻ⁿ
  

• Man dividiert zwei Potenzen mit gleicher Basis:
  

• Basis zusammenfassen, Exponenten subtrahieren: 5³:5²=5¹
  

• Mehr unter Potenzen mit gleicher Basis dividieren ↗
  

aᵐ·bᵐ

• Regel: aᵐ·bᵐ = (a·b)ᵐ
  

• Man multipliziert zwei Potenzen mit gleichem Exponenten
  

• Basen multiplizieren, Exponenten zusammenfassen: 4³·2³=8³
  

• Mehr unter Potenzen mit gleichem Exponenten multiplizieren ↗
  

aᵐ:bᵐ

• Regel: aᵐ:bᵐ = (a:b)ᵐ
  

• Man dividiert zwei Potenzen mit gleichem Exponenten
  

• Basen dividieren, Exponenten zusammenfassen: 10³:5³=2³
  

• Mehr unter Potenzen mit gleichem Exponenten dividieren ↗
  

r⁻ᵐ

• Regel: (a:b)⁻ᵐ = (b:a)ᵐ
  

• Die Basis immer erst als Bruch schreiben.
  

• Die Zahl 8 kann man zum Beispiel schreiben als: 8/1
  

• Minus weglassen, dafür Kehrwert von Basis bilden
  

• Mehr unter Negativer Exponent ↗
  

(aᵐ)ⁿ

• Regel: (aᵐ)ⁿ = aᵐⁿ
  

• Eine Potenz wird als Ganzes wieder potenziert.
  

• Basis gleichlassen, Exponenten multiplizieren: (2³)² = 2⁶
  

• Mehr unter Potenzen potenzieren ↗
  

Potenzturm

• 2^3^4 = 2^81
  

• Immer von rechts rechnen
  

• Erst 3⁴ (gibt 81), dann 2⁸¹
  

• Mehr unter Potenzturm ↗
  

∜a

• Regel: n-te Wurzel aus a = a^(1/n)
  

• n-te Wurzel aus a = a hoch eins-durch-n
  

• Mehr unter n-te Wurzel aus Potenz ↗
  

• Mehr unter r-te Wurzel aus Potenz ↗
  

a⁰

• Regel a⁰=1 für alle a≄0
  

• Mehr unter Hoch Null ↗
  

0⁰

• Regel: 0⁰=↯
  

• Ist nicht definiert (geht nicht)
  

• Mehr unter Null hoch Null ↗
  

Auf- und ableiten

• x² aufgeleitet gibt x³/3 Aufleiten über Potenzregel ↗
  

• x² abgeleitet gibt 2x Ableiten über Potenzregel ↗
  

Tipps

Tipp 1: Langform nutzen

Tipp 2: kürzen können

Aufgaben dazu