Logarithmusrechnung
Übersicht
© 2016
- 2025
Basiswissen
Grundlegende Begriffe und Definitionen werden kurz vorgestellt. Die Logarithmusrechnung ist sozusagen das Potenzrechnen umgekehrt gedacht.
Einführung
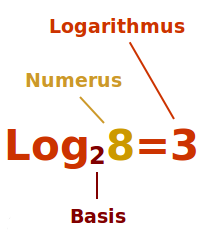
Wenn 2³=8 ist, dann kann man die Zahl 3 als Hochzahl oder Exponent bezeichnen. Der ganze Ausdruck 2³ ist eine Potenz. Und die Zahl 8 ist der Potenzwert. In einer anderen Sprechweise kann man auch sagen, dass die Zahl 3 hier der Logarithmus von 8 zur Basis 2 ist. Der Logarithmus von der 8 zur Basis 2 ist die Hochzahl, die die Basis 2 in den Potenzwert 8 überführt.
Das Rechnen mit Logarithmen erscheint uns heute im Zeitalter der Rechenmaschinen zunächst vielleicht als unnötig umständlich. Aber als die Logarithmusrechnung im 17ten und 18ten Jahrhundert entstand und große Verbreitung fand, was sie eine ganz außerordentlich große Hilfe beim Rechnen.
Man hatte über die Jahrzehnte riesige Tabellenwerke, sogenannte Tafeln, mit fertig berechnete Logarithmen erstelle, zu verschiedenen Basen und mit verschiedenen Genauigkeiten.[1] Wer den Umgang mit solchen Tafeln einmal gelernt hatte, konnte sich damit viel Rechenarbeit ersparen, unter anderem bei der Multiplikation. Betrachten wir ein Beispiel dazu. So könnte ein Ausschnitt einer Tafel von Logarithmen zur Basis 2, gerundet auf die zweite Nachkommastelle, ausgesehen haben:
- Der Logarithmus von 1 zur Basis 2 ist rund: 0,00
- Der Logarithmus von 2 zur Basis 2 ist rund: 1,00
- Der Logarithmus von 3 zur Basis 2 ist rund: 1,58
- Der Logarithmus von 4 zur Basis 2 ist rund: 2,00
- Der Logarithmus von 5 zur Basis 2 ist rund: 2,32
- Der Logarithmus von 6 zur Basis 2 ist rund: 2,58
- Der Logarithmus von 7 zur Basis 2 ist rund: 2,81
- Der Logarithmus von 8 zur Basis 2 ist rund: 3,00
- Der Logarithmus von 9 zur Basis 2 ist rund: 3,17
...
- Der Logarithmus von 30 zur Basis 2 ist rund: 4,91
- Der Logarithmus von 31 zur Basis 2 ist rund: 5,95
- Der Logarithmus von 32 zur Basis 2 ist rund: 5,00
- Der Logarithmus von 33 zur Basis 2 ist rund: 5,04
- Der Logarithmus von 34 zur Basis 2 ist rund: 5,09
- Der Logarithmus von 35 zur Basis 2 ist rund: 5,13
- Der Logarithmus von 36 zur Basis 2 ist rund: 5,17
- Der Logarithmus von 37 zur Basis 2 ist rund: 5,21
- Der Logarithmus von 38 zur Basis 2 ist rund: 5,25
- Der Logarithmus von 39 zur Basis 2 ist rund: 5,29
Solche Tabellen füllten ganze Bücher. Nun kann man die Multiplikation zu einer Addition machen. Wenn man zum Beispiel 5 mal 7 rechnen möchte, kann man zunächst die Logarithmen von 5 und 7 aus der Tabelle ablesen und addieren: 2,32 + 2,81 = 5,13. Nun schlägt man in der Tabelle nach, welche Zahlen am ehesten den Logarithmus 5,13 hat. So findet man die 35 als Ergebnis für die Multiplikation. Beachte, dass man dabei überhaupt nicht multiplizieren muss.
Für die Rechnung 5 mal 7 braucht man natürlich noch keine Logarithmentafeln als Hilfe. Aber wenn man im Jahr 1750 die Zahl 8735 mal der Zahl 7659 rechnen wollte, ging es mit den Logarithmustafel deutlich schneller.[2]
Begriffe
Arten
Grundrechenarten
Spezialverfahren
Diverses
- Logarithmus anschaulich Logarithmusrechnung sprachlich ↗
- Anwendung in der Akustik Dezibel ↗
- Anwendung in der Chemie ph-Wert ↗
Fußnoten
- [1] Johann Heinrich Lambert: Zusätze zu den logarithmischen und trigonometrischen Tabellen, zur Erleichterung und Abkürzung der bey Anwendung der Mathematik vorfallenden Berechnungen. Berlin 1770.
- [2] Und um sogar die Addition überflüssig zu machen, entwickelte man den sogenannten Rechenschieber. Dort könnte man einfach zwei lineale Gegeneinander verschieben. Die Logik der Logarithmusrechnung steckte darin, man müsste so gut wie gar nicht mehr Rechnen. Die Ergebnisse einer Multiplikationen oder Division konnte man ausreichend genau durch bloßes mechanisches Schieben und Ablesen von Zahlen erhalten. Diese Art des Rechnens war noch bis in den Beginn des Computerzeitalters, bis etwa in die 1970er Jahre verbreitet. Siehe mehr dazu unter Rechenschieber ↗