ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Fadenpendelgeschwindigkeit

Versuch

Basiswissen


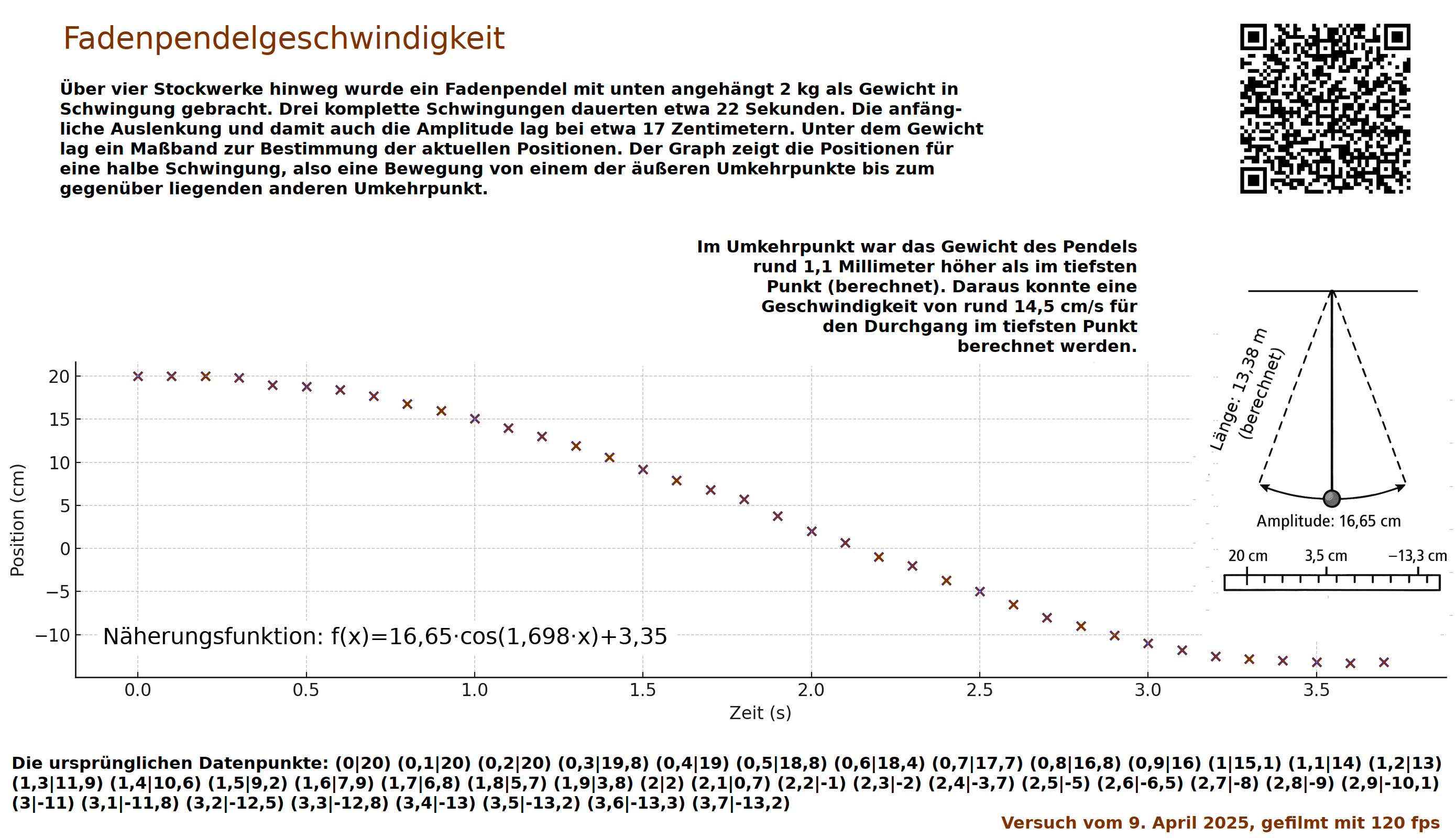
Ein etwa 60 Zentimeter langes Fadenpendel wird aus verschiedenen Starthöhen fallen gelassen. Daran wird beispielhaft gezeigt, wie man die maximale Geschwindigkeit des Pendelgewichts beim Durchgang durch die Position der Ruhelage abschätzen kann.

Geschwindigkeit zu beliebigen Zeitpunkten


Ein Fadenpendel hängt in seinem Ruhezustand senkrecht vom Aufhängspunkt nach unten in der sogenannten Ruhelage. Lenkt man es dann um einen Winkel alpha aus dieser Ruhelag aus, und lässt man es dann frei schwingen, so beschleunigt es zunächst hin zu Ruheposition. Es hat dabei immer eine Geschwindigkeit von in Abhängigkeit von der Zeit t. Nach dem Durchgang durch die Ruheposition wird das Pendel langsamer, bis es den Umkehrpunkt gegenüber dem anfänglichen Startpunkt erreicht hat. Dort durchläuft es die Geschwindigkeit 0 und pendelt dann wieder zurück Richtung Ausgangslage. Die Geschwindigkeit zu jedem beliebigen Zeitpunkt des Pendelvorganges kann über eine Formel berechnet werden:


Mit:


Diese Formel ist im allgemeinem Zusammenhang vorgestellt als Geschwindigkeits-Zeit-Gesetz für eine harmonische Schwingung ↗

vmax: die maximale Geschwindigkeit


Die maximale Geschwindigkeit erreicht die Pendelmasse beim Durchgang durch den tiefsten Punkt der pendelbewegungen. Zu diesem Zeitpunkt muss die ursprüngliche Höhenenergie, die potentielle Energie vom Startpunkt, vollständig in Bewegungsenergie umgewandelt sein. Man kann also die Terme für die Höhen- und für die Bewegungsenergie gleichsetzen:

vmax Rechnerisch



Mit


Die Masse m kann man direkt auf beiden Seiten über eine Äquivalenumformung wegdividieren. Anschließend stellt man um nach der Geschwindigkeit v und erhält:


In Worten: die Geschwindigkeit ist gleich der Wurzel des Doppelten des Produktes aus der Erdfallbeschleunigung und der vertikalen Starthöhe.

Für eine Starthöhe von etwa 0,03 Zentimetern erhält man für ein Pendel der Länge 0,6 Meter eine Durchgangsgeschwindigkeit von etwa 8,5 cm/s.

vmax, gemessen


Die Geschwindigkeit des Fadenpendels nimmt ausgehend von der Anfangsposition sehr schnell zu. Diese Geschwindigkeitsänderung kann das Auge kaum wahrnehmen. Die Geschwindigkeit im tiefsten Punkt der Pendelbewegung ist mit bloßem Auge sehr schwer abzuschätzen.



Das Video zeigt ein Fadenpendel mit einer Länge von 60 cm mit einer anfänglichen Auslenkung von 2°. Die abgeschätzten Werte für die Periodendauer T[1] und die Geschwindigkeit des Pendels im tiefsten Punkt passen gut auf die hier vorgestellten Formeln.

Bei einem kurzen Pendel von etwa 60 cm mit einer geringen Auslenkung von zum Beispiel 2° am Anfang kann man die Geschwindigkeit noch einigermaßen gut mit dem Auge abschätzen. Das wird so gut wie unmöglich bei größeren Auslenkungen und höheren Geschwindigkeiten.

Für eine Starthöhe von 10 Zentimetern oder 0,1 Metern erhält man durch einsetzen und ausrechnen eine Geschwindigkeit von von etwa 1,41 m/s oder 141 cm/s. Entsprechend kann man nun für andere Starthöhen die Geschwindigkeit beim Durchgang durch die Ruheposition berechnen.

vmax, weitere Rechenwerte


Die folgenden Zahlenbeispiele für gerechnete Werte gelten für ein Pendel der Länge 0,6 Meter und bei einer Erdfallbeschleunigung von etwa 10 m/s². Die Auslenkung bezieht sich auf die vertikale Lage in Ruheposition.


Fußnoten