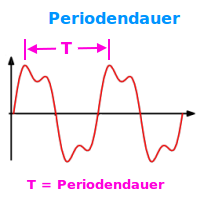
Periodendauer
Physik
© 2016
- 2026
Definition
Von einer Periode spricht man, wenn sich ein Vorgang öfters oder ständig wiederholt. Das Wort wird häufig im Zusammenhang mit Schwingungen und Wellen benutzt. Die übliche Abkürzung ist ein großes T.
Pendelversuch
Nimm einen Faden mit einer Länge von etwa 1 Meter und befestige unten ein kleines schweres Gewicht. Ideal ist zum Beispiel eine Schraubenmutter. Lasse das Gewicht nach unten hängen und versetze diese Fadenpendel dann in Schwingung von links nach rechts. Eine vollständige Bewegung von links nach rechts und wieder zurück zur Ausgangsposition sollte in etwa 2 Sekunden dauern. Das ist die Periodendauer. Siehe auch unter 👉 Pendelversuch
Welle
Wellen bestehen aus vielen einzelnen Teilchens oder Elementen die für sich alleine schwingen. Diese Schwingung setzt sich dabei von Teilchen zu Teilchen mit Zeitverzug im Raum fort. Die Periodendauer einer Welle ist dann definiert als Periodendauer der Schwingung von einem dieser Teilchen (den Oszillatoren). Mehr dazu unter 👉 Periodendauer (Welle)
Beispiele
Faden-, Stangen- oder Stabpendel sowie auch elektrische Schwingkreise: siehe unter 👉 Periodendauern
Synonyme
Fußnoten
- [1] Die Perioden- oder Schwingungsdauer in einer Erklärung aus dem Jahr 1905 (heute noch gültig): "Die Schwingungsdauer t eines Pendels wird ausgedrückt durch die Formel t = 2π√(l/g) oder = π√(l/g), je nachdem man darunter die Dauer einer ganzen oder halben Schwingung versteht (Pendelgesetz), l bedeutet die (reduzierte) Pendellänge, g die Beschleunigung der Schwere (Akzeleration), d. h. die Geschwindigkeit eines frei fallenden Körpers am Ende der ersten Fallsekunde, und, π die Zahl 3,14159, d.h. das Verhältnis des Umfanges eines Kreises zu seinem Durchmesser. " In: Meyers Großes Konversations-Lexikon, Band 15. Leipzig 1908, S. 560-562. Online: http://www.zeno.org/nid/20007228198