ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

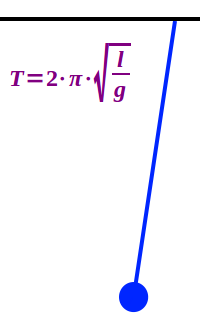
Pendelgesetz

Physik

© 2016 - 2025


Basiswissen · Formel · Legende · In Worten · Beispielrechnung · Beispielversuch · Gültigkeitsbereich · Genauigkeit · Periodendauer · Pendellänge · Erdfallbeschleunigung · Ortsfaktor · Grönlandforschung · Harmonische Schwingung als Verallgemeinerung · Nicht-Fadenpendel · Fußnoten


Basiswissen


T = 2·π·√(l/g) - Mit dem Pendelgesetz[1] als Formel kann man berechnen, wie lange ein Fadenpendel für eine vollständige hin-und-her Schwingung benötigt. Dieses Pendelgesetz geht zurück auf den italienischen Naturforscher Galileo Galilei (1564 –1642)[3]. Hier ist erklärt, wie man mit dem Pendelgesetz die Dauer einer Schwingung berechnet. Das Pendelgesetz kann aus den allgemeineren Zusammenhängen einer sogenannten harmonischen Schwingung hergeleitet werden.



Bildbeschreibung und Urheberrecht
Ein Pendel ist ein Stab oder Faden, an dem unten ein Gewicht hängen kann. Das Pendel ist oben drehbar aufgehängt und kann hin und her schwingen. Diese Bewegung ist der Gegenstand des Pendelgesetzes.☛


Formel


  • T = 2·π·√(l/g)

Legende



In Worten


  • Wenn es zum Beispiel 85 Zentimeter lang ist, dann rechnet man mit 0,85 Metern.
  • Das Ergebnis dieser Multiplikation rechnet man noch mal 2.
  • Das Endergebnis ist die Pendeldauer T in Sekunden.

Beispielrechnung


  • Ein Fadenpendel hat eine Länge von l = 0,65 Metern.
  • Das setzt man in die Formel ein: T = 2·3,14·[Wurzel aus 0,65/10]
  • Das ergibt ausgerechnet: T = 1,6 Sekunden

Beispielversuch


Mit wenig Aufwand kann man leicht ein Fadenpendel selbst herstellen. Und damit lassen sich die hier behandelten Formeln einigermaßen gut überprüfen und anwenden.

An das eine Ende eines Fadens befestigt man dazu einfach ein möglichst kleines und schweres Gewicht. Ideal sind zum Beispiel Muttern von Schrauben aus Metall oder schwere Kugeln mit einem Haken. Mit einer Stoppuhr misst man dann die Zeitdauer für 10 Schwingungen. Teilt man die gemessene Sekundenzahl durch 10, erhält man die Dauer für eine Schwingung in Sekunden.



Ein Beispiel mit einem 0,5-Meter langen Pendel, mit Formel und Messung. In dem Video wird Schritt-für-Schritt gezeigt, wie man die Dauer einer Schwingung berechnet. Am Ende wird der berechnete Wert empirisch, das heißt mit einem Versuch, überprüft.

Mit einer Kamera, etwa von einem Smartphone, kann man den Pendelvorgang filmen und anschließend in Zeitlupe (slow-motion) und mit einer Zeitfunktion (timer) recht detailliert analysieren. Dabei ist es von Vorteil, wenn man die Kamera auf möglichst viele fps (frames per second = Bilder pro Sekunde) einstellen kann. Für viele Filmaufnahmen genügen 30 fps. Für eine möglichst detaillierte Auswertung einer Pendelbewegung sollten es aber schon über 120 oder sogar 240 fps sein. Damit erreicht man eine wesentlich höhere zeitliche Auflösung.

Gültigkeitsbereich


  • Das Gesetz gilt für irgendwo auf der Erde.
  • Das Pendel muss frei in der Luft pendeln können.
  • Die Auslenkung muss gering sein (wenige Grad)[2]

Genauigkeit


  • Je dünner und leicht der Faden, desto besser
  • Je kleiner und schwerer das Gewicht unten, desto besser
  • Je weniger Luft oder auch Wind, desto besser
  • nur für Auslenkungen unter 90 Grad
  • ideal: kleine Auslenkung, Vakuum

Periodendauer


  • Für kleine Auslenkungen[2] gilt:
  • T steht für die Periodendauer in Sekunden:
  • T sagt, wie lange das Pendel für einmal ganz hin und her braucht.
  • T wird Pendel-, Schwingungs- oder Periodendauer genannt.



Zur Definition einer Schwingung: eine Schwingung von rechts, über links zurück nach rechts[5]

  • Rechne 1 geteilt durch T in Sekunden, das gibt die Frequenz in Hertz.
  • Das heißt: der Kehrwert der Periodendauer ist die Frequenz.
  • Die Frequenz wird manchmal auch Schwingungszahl genannt.
  • Auf dem Mond wäre g anders, nämlich nur 1,62 m/s².

Pendellänge


Stellt man das Pendelgesetz um nach der Pendellänge l kann man durch Einsetzen der bekannten Erdfallbeschleunigung g (etwa 9,81 m/s²), des Wertes für die Kreiszahl Pi (etwa 3,14) und der gemessenen Periodendauer T die Länge des Pendels berechnen.

  • T = 2·π·√(l/g) | umstellen nach der Länge l
  • l = (T/(2·π)²·g

In Worten: Man teilt die gemessene Periodendauer in Sekunden durch das Doppelte von Pi. Dann quadriert man dieses Zwischenergebnis, rechnet es also einmal mit sich selbst mal. Das Ergebnis davon wird am Ende noch mit der Erdfallbeschleunigung von etwa 9,81 m/s² malgenommen. Das Endergebnis ist dann die Länge l des Fadenpendels.

Zahlenbeispiel: Angenommen ein Pendel benötigt für eine ganze Periodendauer T (einmal hin und wieder zurück) genau 10 Sekunden, dann setzt man ein und erhält für T = 10 s:

  • l = (T/(2·π)²·g
  • Mit T = 10 s, π ≈ 3,14 und g = 9,81 m/s²:
  • l ≈ (10/6,28)²·9,81
  • l ≈ 25 Meter

Mit einem ausreichend langen Fadenpendel kann man also einigermaßen gut auch Höhenmessungen vornehmen, etwa indem man ein langes Pendel von einer Brüche schwingen lässt. Siehe dazu den Artikel Rolleftal-Viadukt [Messbeispiel] ↗

Erdfallbeschleunigung


  • Wenn man weiß, wie lang das Fadenpendel ist, ...
  • dann kann man damit die Periodendauer ausrechnen.
  • Kennt man die Periodendauer (etwa durch Messung), dann ...
  • kann man durch Umstellen die Fadenlänge ausrechnen.
  • Kennt man die Länge und die Periodendauer, dann kann ...
  • man durch Umrechnen die Erdbeschleunigung g ausrechnen.
  • Die Erdbeschleunigung ist zahlengleich mit dem Ortsfaktor.

Ortsfaktor


  • Mit Hilfe eines Pendels kann man den Ortsfaktor bestimmen.
  • Man misst die Periodendauer in einem Versuch möglichst genau.
  • Man misst die Fadenlänge und setzt die Werte in das Pendelgesetz ein.
  • Dann löst man nach g auf. g ist die Fallbeschleunigung in m/s².
  • g ist aber auch zahlengleich mit dem Ortsfaktor N/kg.
  • Hat man g bestimmt, kennt man also auch den Ortsfaktor.

Grönlandforschung


  • Der Meteorologe Alfred Wegener machte mehrere Expeditionen nach Grönland.
  • Ein Ziel der Expedition war die Messung der Eisdicke.
  • Das Eis war zu dick, um es mit Bohrungen zu untersuchen.
  • Die Forscher stellten deshalb ein Pendel auf die Oberfläche.
  • Sie maßen dann sehr exakt die Pendeldauer.
  • Daraus konnten sie rückwärts die Erdfallbeschleunigung berechnen.
  • Und daraus wiederum zogen sie Rückschlüsse auf den Untergrund.
  • Das Eis in Grönland hat eine maximale Dicke von maximal 3367 Metern (2020).

Harmonische Schwingung als Verallgemeinerung


Als harmonische Schwingung bezeichnet man jede Schwingung, bei der die momentane Rückstellkraft des schwingenden Körpers hin zu seiner Ruhelage immer proportional zur momentanen Auslenkung ist. Wenn das Pendel also in einem Punkt A doppelt so weit von der Ruhelage entfernt ist wie in einer anderen Position B, dann ist die wirkende Rückstellkraft in A auch doppelt so groß wie in B. Mit diesem Ansatz lassen sich ein Weg-Zeit und ein Geschwindigkeits-zeit-Gesetz für allgemeine solche Schwingungen aufstellen. Das idealisierte Fadenpendel, auch mathematisches Pendel genannt, ist dann ein Sonderfall. Zur mathematischen Herleitung siehe dazu den Artikel über die Harmonische Schwingung ↗

Nicht-Fadenpendel


Das hier beschrieben Pendelgesetz gilt nur für ideale Fadenpendel. Neben dem Fadenpendel gibt es noch andere Pendel. Für sie gelten andere Formeln. Ein typisches Beispiel ist das Balkenpendel ↗

Fußnoten


  • [1] Das Pendelgesetz in einer Erklärung aus dem Jahr 1905 (heute noch gültig): "Die Schwingungsdauer t eines Pendels wird ausgedrückt durch die Formel t = 2π√(l/g) oder = π√(l/g), je nachdem man darunter die Dauer einer ganzen oder halben Schwingung versteht (Pendelgesetz), l bedeutet die (reduzierte) Pendellänge, g die Beschleunigung der Schwere (Akzeleration), d. h. die Geschwindigkeit eines frei fallenden Körpers am Ende der ersten Fallsekunde, und, π die Zahl 3,14159, d.h. das Verhältnis des Umfanges eines Kreises zu seinem Durchmesser." In: Meyers Großes Konversations-Lexikon, Band 15. Leipzig 1908, S. 560-562. Online: http://www.zeno.org/nid/20007228198
  • [2] Das hier beschriebene Pendelgesetzt gilt umso genauer, je kleiner die Auslenkung eines Pendels ist. Bei wenigen Grad Auslenkung ist der Fehler so klein, dass er mit üblichen Methoden nicht mehr gemessen werden kann. Galileo Galilei hatte - fälschlicherweise - behaupt, dass die Pendeldauer für jede beliebige Auslenkung gleich sei. Zu dieser Behauptung kam er durch eine unzulässige Extrapolation (Verallgemeinerung) von Messergebnissen. Jürgen Teichmann: Wandel des Weltbildes. Astronomie, Physik und Meßtechnik in der Kulturgeschichte. Mit Beiträgen von Volker Bialas und Felix Schmeidler. Wissenschaftliche Buchgesellschaft. Darmstadt. Dort wird Galileis Falschbehauptung im Abschnitt "Gedankenexperiment und Realexperiment" auf Seite 142 kurz behandelt.
  • [3] Historisch geht das hier beschriebene Gesetz auf Galileo Galilei zurück: "Ab 1585 befaßte sich Galileo Galilei (1564 –1642), italienischer Mathematiker, Physiker und Astronom) mit Pendelbewegungen und fand die Pendelgesetze. 1629 schrieb G. Galilei die Pendelgesetze nieder: T = 2 π √l/g, wobei die Erdbeschleunigung g als Naturkonstante betrachtet wird." In: Joachim Höpfner: Absolute Bestimmung der Schwere mit Reversionspendeln in Potsdam 1898 bis 1904 und 1968 bis 1969. Erschienen bei der Deutschen Gesellschaft für Chronometrie, Jahresschrift. 2012. 2012, Bd. 51, S. 101- 114. Dort die Seite 103.