ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Arithmetisches Mittel

x̄

© 2016 - 2025


Basiswissen · Berechnung · Deutung als gleichmäßiger Summenbeitrag · Deutung als Datenschwerpunkt · Rechen-Beispiel · Formelzeichen · Alltagssprache · Was ist der Unterschied zum Erwartungswert? · Welche Bedeutung hat der Durchschnitt in der Physik? · Fußnoten · Versuche zum arithmetischen Mittel · Synonyme


Basiswissen


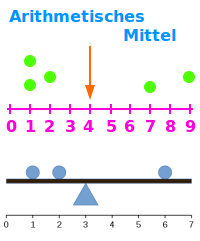
Das arithmetische Mittel, auch Durchschnitt genannt, ist anschaulich gesprochen die gefühlte Mitte oder der Schwerpunkt von mehreren Zahlen. Der Mittelwert gehört also immer zu einer Liste von Zahlen. Die Berechnung und Bedeutung sind hier kurz erklärt.



Bildbeschreibung und Urheberrecht
Das arithmetische Mittel der Zahlen 1;1;2;7 und 9 ist genau 4. Die 4 wäre auch der Schwerpunkt dieser Zahlen auf eine Waagbalken. © Gunter Heim user Maphry on Wikimedia Commons ☛


Berechnung


  • Alle Zahlen zusammenaddieren und durch die Anzahl teilen.
  • Beispiel: 1, 2 und 3: addieren gibt: 6
  • Durch die Anzahl (hier 3) teilen: gibt 2
  • Die Zahl 2 ist das arithmetische Mittel von 1, 2 und 3.

Deutung als gleichmäßiger Summenbeitrag


Das arithmetische Mittel kann man anschaulich-praktisch als gleichmäßigen Beitrag aller Zahlen zur gemeinsamen Summe, wenn jede Zahl gleich viel beiträgen müsste. Als Beispiel: man hat 10 Zahlen die zusammengerechnet 40 ergeben. Wenn jede der zehn Zahlen gleich viel zu dieser Summe 40 beitragen würde, wie groß wäre dann jede der Zahlen? Antwort: 4. Die 4 ist dann auch das arithmetische Mittel der 10 Zahlen.

Deutung als Datenschwerpunkt


Man stelle sich die Zahlen als Kugeln auf einer Zahlengeraden vor. Das arithmetische MIttel der Zahlen ist dann diejenige Stelle auf der Zahlengeraden unter die man einen Finger halten könnte und die Gerade wäre dann perfekt ausbalanciert. Die Stelle ist dann physikalisch-anschaulich gesprochen der Datenschwerpunkt ↗

Rechen-Beispiel


  • Die Zahlen wären 10; 15; 25 und 30.
  • Alles zusammenaddieren gibt: 80.
  • Die Anzahl der Zahlen ist 4.
  • Also: 80 durch 4 rechnet, gibt 20.
  • Das arithmetische Mittel ist: 20.

Formelzeichen


  • Üblich ist ein x mit Querstrich darüber, das x quer ↗

Alltagssprache


  • Umgangssprachlich üblich sind folgende Wendungen:
  • Im Schnitt flogen sie in einer Höhe von 10 km.
  • Im Mittel wogen die Muscheln 24 Gramm.
  • Der Mittelwert lag bei 210 Sekunden

Was ist der Unterschied zum Erwartungswert?


In der Stochastik, das heißt der Wahrscheinlichkeitsrechnung, gibt es auch das Wort Erwartungswert, oft mit einem kleinen µ (my) abgekürzt. Während man das arithmetische Mittel immer für eine begrenzte Anzahl von Zahlen berechnet, zum Beispiel echte Messwerte, ist der Erwartungswert immer nur eine rein theoretische Zahl: das arithmetische Mittel, das man im Idealfall erwarten würde, wenn ein Versuch vollkommen wie von der Theorie gefodert abläuft. Lies mehr dazu unter Erwartungswert ↗

Welche Bedeutung hat der Durchschnitt in der Physik?


Physikformeln und Naturgesetze gelten oft nur für Durchschnittswerte, also das arithmetische Mittel von vielen Messwerten. Dieser Aspekt kommt bei fast allen Naturgesetzen zum Tragen[1]. Siehe auch Naturgesetz ↗

Fußnoten


  • [1] Franz Serafin Exner: Physikalische Gesetze als Durchschnittsgesetze. Fragliche Gültigkeit derselben in kleinen Gebieten (7. Vorlesung). In: Vorlesungen über die physikalischen Grundlagen der Naturwissenschaften. Deuticke, Wien 1919, OBV. Seite 665 — 670. Siehe auch Grundlagen der Naturwissenschaften (Exner) ↗

Versuche zum arithmetischen Mittel



Synonyme