Quartische Funktion
x^4
© 2016
- 2025
Basiswissen
Ganzrationale Funktion mit höchstens x hoch 4: als quartisch bezeichnet man eine Funktion, die man in die Form f(x) = a·x^4 + b·x^3 + c·x^2 + d·x + e bringen kann. Ein anderer, gleichbedeutender Name ist ganzrationale Funktion vierten Grades. Das Wort quartisch steht für 4 und bezeichnet die höchste vorkommende Potenz der unabhängigen Variablen x.
Beispiele
- f(x) = 8x⁴-6x³+4x²-12
- f(x) = 7x⁴-6x³-4x²
- f(x) = 6x⁴+6x³
- f(x) = 5x⁴
- f(x) = x⁴
Definition
- f(x) = ax^4 + bx^3 + cx^2 + dx + e
- Quartische Funktionen gehören zu den ganzrationalen Funktionen
- b, c, d und e dürfen 0 sein, a aber nicht.
- Jede Funktion deren Funktionsterm man in ...
- diese Form bringen kann heißt quartisch.
Biquadratisch
- Kann man umformen in f(x) = ax^4 + bx² + c, dann ...
- heißt die quartische Funktion auch eine biquadratische.
- Biquadratische Funktionen sind oft besonders einfach.
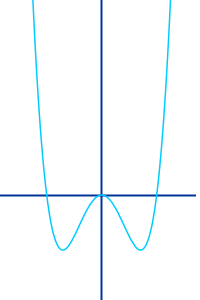
Graph
- Der Graph heißt Parabel vierter Ordnung ↗
- Er kann aussehen wie eine normale Parabel.
- Er kann auch aussehen wie ein Backenzahn.
- Er kann bis zu vier Nullstellen haben.
- Er kann auch gar keine NS haben.
Synonyme
- Quartische Funktion
- ganzrationale Funktion vierten Grades
- Polynomfunktion vierten Grades