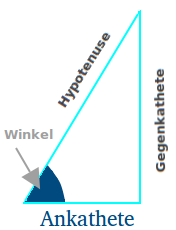
Ankathete berechnen
Anleitung
© 2016
- 2025
Basiswissen|
Kurzübersicht|
Was ist eine Kathete an sich?|
Was ist die Ankathete?|
Wie berechnet man eine Ankathete?|
1. Methode: Ankathete über den Tangens berechnen|
2. Methode: Ankathete über den Cosinus berechnen|
3. Methode: Ankathete über Pythagoras berechnen|
Gelten diese Regeln hier immer?
Basiswissen
Die Ankathete ist immer eine der zwei kürzeren Seiten in einem rechtwinkligen Dreieck. Man kann sie mit dem Cosinus, Tangens oder auch dem Satz des Pythagoras berechnen. Hier stehen verschiedene Methoden, wie man die Länge einer solchen Ankathete berechnen kann.
Kurzübersicht
- 1. Man kennt den Länge der anderen Kathete und den Winkel gegenüber 👉 Ankathete über Tangens
- 2. Man kennt den Länge der Hypotenuse und anliegenden Winkel 👉 Ankathete über Cosinus
- 3. Man kennt die Länge der zwei anderen Seiten 👉 Kathete über Pythagoras
Was ist eine Kathete an sich?
- Katheten gibt es nur in rechtwinkligen Dreiecken
- Eine Kathete ist immer eine der zwei Seiten an dem rechten Winkel.
- Der rechte Winkel ist immer der 👉 90-Grad-Winkel
- Die zwei Katheten sind immer auch die zwei kürzeren Seiten im Dreieck.
- Siehe auch 👉 Kathete
Was ist die Ankathete?
- Eine Ankathete gehört immer zu einem Winkel im Dreieck.
- Dieser Winkel darf aber nicht der 90°-Winkel sein, es muss einer der beiden anderen Winkel sein.
- Einen solchen Winkel muss man gegeben haben oder ihn sich selbst auswählen.
- Man kann diesen Winkel dann zum zum Beispiel α (kleines Alpha) nennen.
- Die Ankathe von α ist dann die Kathete, die direkt an α liegt.
- Die Ankathete des Winkels α ist dann auch ein 👉 Schenkel [von α]
- Mehr zur Definition unter 👉 Ankathete
Wie berechnet man eine Ankathete?
Die Ankathete zu berechnen heißt meist, dass man ihre Länge, zum Beispiel in Zentimetern oder Metern, bestimmen soll. Dazu gibt es verschiedene Methoden und Formeln. Diese sind jetzt kurz vorgestellt.
1. Methode: Ankathete über den Tangens berechnen
- Der Winkel α hat immer eine Gegenkathete und eine Ankathete.
- Und ein Winkel α hat immer auch einen Tangenswert.
- Diesen Tangenswert findet man z. B. in der 👉 Tangenstabelle Grad
- Dann rechnet man:
- Die Länge der Gegenathete geteilt durch den Tangens von α.
- Das Ergebnis dieser Rechnung ist die Länge der gesuchten Ankathete.
- Beispiel: die Gegenkathete hat eine Länge von 4 Metern.
- Der Winkel α ist zum Beispiel 20°, dann ist tan(20°) etwa 0,36 (aus Tabelle).
- Man rechnet: 4 Meter geteilt durch 0,36. Das gibt etwa 11 Meter.
- 11 Meter ist dann die Länge der gesuchten Ankathete.
- Lies mehr dazu unter 👉 Ankathete über Tangens
2. Methode: Ankathete über den Cosinus berechnen
- Der Winkel α hat immer eine Hypotenuse und eine Ankathete.
- Die Hypotenuse ist immer die längste Seite im Dreieck.
- Und ein Winkel α hat immer auch einen Cosinuswert.
- Diesen Cosinuswert findet man z. B. in der 👉 Cosinustabelle Grad
- Dann rechnet man:
- Hypotenuse mal Cosinus gibt die Ankathete:
- Die Hypotenuse ist die längste Seite in dem Dreieck.
- Man kennt einen der beiden nicht-90°-Winkel in dem Dreieck.
- Angenommen einer dieser Winkel sei 70 Grad.
- Angenommen die Länge der Hypotenuse sei 20 Meter.
- Man rechnet dann immer: Hypotenuse mal Cosinus des Winkels.
- Also: 20 Meter mal Cosinus von 70 Grad, das gibt etwa 6,8 Meter.
- 6,8 Meter ist die Länge der gesuchten Ankathete.
- Lies mehr dazu unter 👉 Ankathete über Cosinus
3. Methode: Ankathete über Pythagoras berechnen
- a²+b² = c² ist der 👉 Satz des Pythagoras
- a und b stehen hier für die Länge der beiden Katheten.
- Will man die Länge b berechnen, stellt man um: b=√(c²-a²)
- Wenn b alos die gesuchte Länge einer der zwei Katheten ist,
- und c ist die Länge der Hypotenuse und a die Länge der anderen Kathete,
- dann rechnet man: c hoch zwei minus a hoch zwei und daraus die Wurzel.
- Das Ergebnis ist dann die Länge b der gesuchten Kathete.
- Mehr unter 👉 Kathete über Pythagoras
Gelten diese Regeln hier immer?
Die Regeln hier gelten für alle rechtwinkligen in der sogenannten ebenen Geometrie immer. Die übliche Geometrie aus der Schule ist meistens diese ebene Geometrie. Man zeichnet Gebilde auf gedanklich flachen Flächen (Papier auf Tisch, Zeichenbrett etc.) oder dreidimensional in einem sogenannten Euklidischen Raum. Es gibt aber auch eine sogenannte sphärische Geometrie. Sphärisch meint hier so viel wie kugelig. Die Geometrie auf der Oberfläche von einem Globus etwa wäre sphärisch. Dort gelten dann viele Gesetze nicht mehr. In der sphärischen Geometrie kann ein Dreieck zum Beispiel drei rechte Winkel haben. Siehe als beispielhaften Einstieg in die sphärische Geometrie das 👉 Galapagos-Dreieck