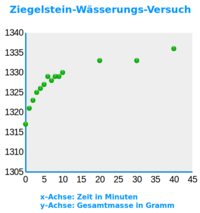
Ziegelstein-Wässerungs-Versuch
Materialkunde
Basiswissen
Ein trockener Ziegelstein wurde gewogen: 1317 Gramm. In Wasser gelegt, nahm er innerhalb von 10 Minuten gut 13 Gramm oder Milliliter Wasser auf. Nach gut einer Woche hatte er insgesamt 81 Milliliter Wasser aufgesogen. Hier stehen die genauen Messdaten sowie Hinweise für eine mathematische Formel.
Vor dem Wässern
Die Maße des Ziegels sind: Länge 200 mm, Breite 65 mm und Höhe etwa 50 mm. Die Kanten waren nicht scharf sondern an vielen Stellen etwas eingebrochen. Im Folgenden steht hier nur die Rohdatenliste. Der Ziegelstein wurde dann in kurzen aufeinanderfolgenden Zeiträumen vollständig in ein Wasserbecken gelegt. Wie schnell dringt Wasser ein?
Rohdaten
- 0 Minuten Wässerung ⭢ 1317 Gramm
- 1 Minute Wässerung ⭢ 1321 Gramm
- 2 Minuten Wässerung ⭢ 1323 Gramm
- 3 Minuten Wässerung ⭢ 1325 Gramm
- 4 Minuten Wässerung ⭢ 1326 Gramm
- 5 Minuten Wässerung ⭢ 1327 Gramm
- 6 Minuten Wässerung ⭢ 1329 Gramm
- 7 Minuten Wässerung ⭢ 1328 Gramm
- 8 Minuten Wässerung ⭢ 1329 Gramm
- 9 Minuten Wässerung ⭢ 1329 Gramm
- 10 Minuten Wässerung ⭢ 1330 Gramm
- 20 Minuten Wässerung ⭢ 1333 Gramm
- 30 Minuten Wässerung ⭢ 1333 Gramm
- 40 Minuten Wässerung ⭢ 1336 Gramm
- 4320 Minuten Wässerung ⭢ 1392 Gramm[3 Tage später]
- 9930 Minuten Wässerung ⭢ 1398 Gramm[7 Tage später]
Nachverfolgung
Nach Abschluss der obigen Versuchsreihe - am 12. November 2021 um 17.30 Uhr - wurde der Ziegelstein in einem Mini-Aquarium belassen, wo er vollständig unter der Wasseroberfläche lag.
Physikalisch: beschränkt
Spätestens wenn alle Poren des Ziegelsteins Wasser aufgenommen haben, ist ist eine weitere Gewichtszunahme nicht mehr möglich. Physikalisch gesehen ist die Zunahme der Ziegelsteinmasse nach oben begrenzt, man sagt auch beschränkt. Weitere solche Beispiele stehen unter nach oben beschränkte Wachstumsprozesse ↗
Mathematisch: exponentiell
Trägt man die Messwerte aus der Tabelle oben in eine xy-Koordinatensystem mit x als Zeit und y als Ziegelsteinmasse ein, dann entsteht von der Form her mehr oder minder eine Exponentialkurve. Als mathematisches Modell geeignet ist wahrscheinlich die exponentielle Sättigungsfunktion ↗
