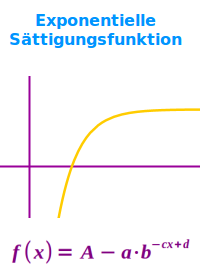
Exponentielle Sättigungsfunktion
Definition
© 2016
- 2025
Basiswissen
f(x) = 4 - 2^(-x + 5): der Graph dieser Funktion steigt erst steil an, flacht dann von links nach rechts gehend stark ab und wird niemals den Funktionswert 4 übersteigen. Das ist hier allgemein erklärt.
Grundbauplan
- f(x) = A - a·b^(-c·x + d)
Grundidee
Vom festen Wert A, dem Sättigungswert, wird ein verändlicher Wert abgezogen: a·b^(-c·x + d). Dieser Term, der vom Sättigungswert A abgezogen ist, ist damit das, was noch bis zur Sättigung fehlt. Das was fehlt nennt man auch auch Manko (vergleiche französisch: manque). Der Term a·b^(-c·x + d) ist also das sogenannte Sättigungsmanko ↗
Legende
- A = wird nie überschritten und heißt auch Sättigungswert oder obere Schranke ↗
- a = ist das Sättigungsmanko wenn der Exponent den Wert 0 hat: streckt oder stauch den Graphen
- b = ist der Faktor mit dem das Sättigungsmanko abnimmt.
- c = Stärke der Abnahme des Sättigungsmankos
- d = Verschiebt den Graphen parallel zur x-Achse.
Sachbeispiele
- Ein Ziegelstein nimmt Wasser auf Ziegelstein-Wässerungs-Versuch ↗
- Ein Kondensator und elektrische Ladung Kondensatoraufladung ↗
- Ein Hausmodell wird aufgeheizt Hausheizversuch ↗
Fachworte
- Der maximale oberste Wert Sättigungswert ↗
- Was bis dahin fehlt Sättigungsmanko ↗