Basiswissen

Zahlen in irgendeine Pluskette zerlegen

• Grunschule:
  

• Bei Zahlen meint zerlegen oft: in eine Pluskette umwandeln:
  

• Die 3 kann man zerlegen in eine 2 und eine 1, denn: 2+1 = 3
  

• Die 5 kann man zerlegen in eine 4 und eine 1, denn: 4+1 = 5
  

• Die 5 kann man zerlegen in eine 3 und eine 2, denn: 3+2 = 5
  

• Die 5 kann man zerlegen in eine 3½ und eine 1½, denn 3½+1½=5
  

• Mehr unter Zahlzerlegung ↗
  

Zahlen nach Stellenwerten zerlegen

• Grundschule:
  

• Man kann Zahlen auch in Tausender, Hunderter, Zehner und Einer zerlegen.
  

• Die 2311 zerlegt in Tausender, Hunderter, Zehner und einer gibt:
  

• Zwei Tausender
  

• Drei Hunderter
  

• Ein Zehner
  

• Ein Einer
  

• Siehe auch Stellenwerttafel ↗
  

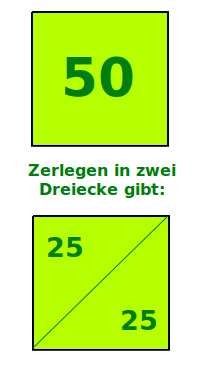
Flächenberechnung über Zerlegen

• Komplzierte Flächen zerlegt man oft in einfachere Teilflächen.
  

• Die Gesamtfläche ist dann aus den Teilen zusammengesetzt.
  

• Lies mehr dazu unter zusammengesetzte Flächen berechnen ↗
  

Terme in Linearfaktoren zerlegen

• Dieses Verfahren spielt beim Lösen von Gleichungen eine Rolle.
  

• Es findet damit auch Anwendung bei der Nullstellenbestimmung.
  

• Man hat einen Funktionsterm, den man in eine Malkette zerlegt.
  

• Die Malkette besteht dann ausschließlich aus linearen oder konstanten Gliedern.
  

• Beispiel: 0 = x²-4 wird zerlegt in: 0 = (x+2)·(x-2)
  

• Siehe auch unter Polynomdivision ↗
  

Höhere Mathematik

• In der Zahlentheorie gibt es den Begriff der Zahlpartition.
  

• Das meint, dass man eine Zahl in natürliche Zahlen zerlegt.
  

• Man darf die 5 dann zerlegen in 4 und 1, nicht aber in 3½ und 1½.
  

• Mehr dazu unter Zahlpartition ↗
  

Ingenieurwesen

• Oft müssen Spannungen, Temperaturen etc. in Bauteilen berechnet werden.
  

• Dazu werden die Bauteile oft gedanklich in einzele Raumelememente zerlegt.
  

• Lies mehr unter Finite-Elemente-Methode ↗