ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

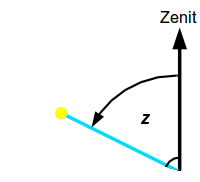
Zenitwinkel

Astronomie

© 2016 - 2025


Basiswissen · Ausführliche Definition · Erklär-Skizze zum Zenitwinkel · Was ist das Gegenteil von einem Zenitwinkel? · Der Zenit- und der Höhenwinkel · Was sind Komplementärwinkel? · Den Zenitwinkel mit Körperteilen schätzen · Den Zenitwinkel mit einem Astrolabium messen · Den Zenitwinkel mit einem Pendelquadranten bestimmen · Fußnoten


Basiswissen


Man blickt senkrecht nach oben, also Richtung Zenit. Wenn man dann von dieser Blickrichtung aus den Kopf einen bestimmten Winkelbetrag nach unten dreht, um einen tieferen Punkt anzuvisieren, dann ist dieser Winkel nach unten der Zenitwinkel[1], auch Zenitdistanz[2] oder Zenitabstand[3] genannt. Blickt man etwa waagrecht Richtung Horizont wäre der Zenitwinkel damit 90°. Das wird hier Schritt-für-Schritt erklärt.



Bildbeschreibung und Urheberrecht
Wie weit muss man den Kopf nach unten drehen, wenn man vorher senkrecht nach oben geblickt hat? Die Antwort auf diese Frage ist der Zenitwinkel☛


Ausführliche Definition


  • Ein Winkel besteht aus einem spitzen Punkt und zwei Geraden, die sich dort treffen.
  • Man kan sich als Beispiel einen großen Buchstaben V vorstellen.

Man stelle sich vor, man steht irgendwo auf der Erdoberfläche. Man richtet den Blick auf einen bestimmten Punkt irgendwo am Himmel. Das könnte ein Stern, ein Vogel oder die Sonne sein. Der Kopf ist der Scheitel des Winkels, also die Spitze der zwei Schenkellinien. Die gedachte Linie von Kopf zu dem Punkt am Himmel ist der eine Schenkel. Jetzt blickt man senkrecht nach oben in den Himmel. Die Richtung, in die man jetzt siehst gibt den anderen Schenkel des Winkels. Der gedachte Punkt senkrecht über einem ist der Zenit. Diese beiden Sichtlinien, die von Kopf ausgehen, bilden den Zenitwinkel. Je näher etwas zum Horizont hin ist, desto größer ist also der Zenitwinkel.

Erklär-Skizze zum Zenitwinkel


  • Skizziere ein Koordinatensystem.
  • Die x-Achse soll 10 cm lang sein (links nach rechts)
  • Die y-Achse soll 100 cm hoch sein (unten nach oben)
  • Bei Punkten gilt: (x-Wert|y-Wert).
  • Trage den Punkt S (8|0) ein.
  • In diesem Punkt ist gedanklich unser Auge.
  • Dieser Punkt ist auch der Scheitel des Winkels.
  • Trage den Punkt Z (8|8) ein.
  • Von S aus gesehen läge Z in Richtung Zenit.
  • Verbinde S und Z.
  • Trage jetzt den Punkt V (2|10) ein.
  • Dies könnte zum Beispiel ein Vogel sein.
  • Ziehe eine Linie von S nach V.
  • Miss den Winkel zwischen den beiden Linien.
  • Der Winkel sollte ungefähr 47 Grad sein.
  • Das ist der Zenitwinkel.

Was ist das Gegenteil von einem Zenitwinkel?



Der Zenit- und der Höhenwinkel


In der Astronomie wurden zur Angabe der Höhenlage eines Himmelskörpers sowohl der Zenitwinkel als auch der Höhenwinkel gemessen. Der Höhenwinkel wird auch als Elevation[2] oder Altitude bezeichnet. Ein Punkt direkt senkrecht über einem, also im Zenit, hat einen Zenitwinkel von 0° und einen Höhenwinkel von 90°. Umgekehrt hat ein Punkt direkt am Horizont einen Horizontwinkel von 0° und einen Zenitwinkel von 90°. Ein Punkt dazwischen, etwa mit einem Höhenwinkel von 20° nur wenig über dem Horizont, hätte einen Zenitwinkel von 70°. Es gilt: Zenit- und die Höhe als Winkel ergeben zusammenaddiert immmer 90°[3]. Also gilt auch: 90° minus Zenitwinkel gleich Höhe; und 90° minus Höhen gleich Zenitwinkel.

Was sind Komplementärwinkel?


Zwei Winkel, die aufaddiert immer 90° ergeben, nennt man in der Geometrie Komplementärwinkel. Der Zenitwinkel und die Elevation aus der Astronomie sind solche Komplementärwinkel ↗

Den Zenitwinkel mit Körperteilen schätzen


Eine gute erste Einschätzung von der ungefähren Größe eines Zenitwinkels kann man mit Hilfe der eigenen Körperteile bekommen. Man streckt den Arm ganz. Dann überdecken verschiedene Figuren, die man mit Hand und Fingern machen kann, verschieden große Winkel am Himmel[5]. Wenn ein Ende der Hand- oder Fingerfigur am Zenit liegt, gibt das gegenüberliegende Ende der Figur den gewünschten Winkelabstand:

  • Bei ausgestrecktem Arm je nach Körperbau etwa 17 bis 20° für eine große Spanne ↗

Den Zenitwinkel mit einem Astrolabium messen


Heute unüblich aber früher gebräuchlich waren die Astrolabien, kleine runde Scheiben mit einer Visierhilfe. Man konnte sie frei pendelnd von der Hand herabhängen lassen. Damit bildeten sie automatisch eine Lotlinie senkrecht nach unten. Visierte man dann einen Himmelskörper an, konnte man auf einer Skala direkt die Poldistanz ablesen. Siehe auch Astrolabium ↗

Den Zenitwinkel mit einem Pendelquadranten bestimmen


Mit einem einfachen Pendelquadranten kann man einen Himmelskörper durch ein Rohr oder eine andere Visierhilfe anpeilen. An einer Skala kann man dann direkt die sogenannte Horizonthöhe oder Elevation ablesen, also die Höhe des Himmelskörpers über dem Horizont als Winkel. Da nun die Poldistanz als Winkel und die Horizonthöhe als Winkel sogenannte Komplementärwinkel sind, ergeben sie zusammenaddiert für einen Himmelskörper immer 90°. Rechnet man also 90° minus den mit dem Pendelquadranten gemessenen Horizontwinkel, hat man direkt die gesuchte Poldistanz. Siehe auch Pendelquadrant ↗

Fußnoten


  • [1] Zenitwinkel erwähnt in: "Tachymetrie, Tacheometrie, Celerimensura, Schnellmessung, ein Messungsverfahren, bei dem die Lage- und Höhenmessungen gleichzeitig ausgeführt werden durch Bestimmung der Horizontalrichtungen, durch Distanzmessung (s. Distanzmesser) sowie durch Beobachtung von Höhen- oder Zenitwinkel oder durch unmittelbare Messung der Höhenunterschiede." In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 8 Stuttgart, Leipzig 1910., S. 403-411. Online: http://www.zeno.org/nid/20006138195
  • [2] "Zenitdistanz ist derjenige Winkel, welchen die Richtung nach einem bestimmten Punkte hin mit der Lotrichtung am Beobachtungspunkt einschließt. Die Zenitdistanz ist die Ergänzung des Höhenwinkels (der Elevation) zu 90°. In der praktischen Meßkunde mißt man mit Vorteil die Zenitdistanz, da diese sich ohne Rücksicht auf die Lotlinie selbst finden läßt, aus der Differenz der beiden Ablesungen an einem Höhenkreis, die man bei Fernrohr rechts und Fernrohr links erhält unter der alleinigen Voraussetzung, daß die Lage der Nullpunktlinie der Ablesevorrichtungen gegenüber dem Horizont konstant geblieben ist. – Bei cölestischen Messungen unterscheidet man scheinbare und wahre Zenitdistanz. Die erstere ist um die Wirkung der Strahlenbrechung (Refraktion, s.d.) kleiner und um den Betrag der Parallaxe (s.d.) größer als die wahre Zenitdistanz, d.h. als die auf den Erdmittelpunkt bezogene. – Die Messung von Zenitdistanzen von Gestirnen wird in der Astronomie zur Bestimmung der Koordinaten des Beobachtungsortes viel benutzt." Verfasst von Ambronn. In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 8 Stuttgart, Leipzig 1910., S. 982. Online: http://www.zeno.org/nid/20006150926
  • [4] "Zenitdistanz oder Scheitelabstand eines Gestirns, der Bogen eines größten Kreises zwischen dem Z. und dem Gestirn, senkrecht zum Horizont." In:
Brockhaus' Kleines Konversations-Lexikon, fünfte Auflage, Band 2. Leipzig 1911., S. 1019. Online: http://www.zeno.org/nid/20001696424
  • [5] Bücher zur Astronomie machen hier verschiedene Angaben. Tests mit verschieden alten Personen in einer Lernwerkstatt in Aachen (z. B. im Jahr 2023) führten zu Abweichungen, die aber immer unter 20 % der angegeben Literaturwere blieben. Siehe auch Winkelschätzung ↗