Symmetrische Matrix
Physik
© 2025
Definition
Als symmetrisch bezeichnet man jede Matrix für die ihre Einträge spiegelsymmetrisch zur Hauptdiagonalen sind. Die Hauptdiagonale geht von oben links nach unten rechts. Die Einträge der Hauptdiagonalen können beliebig sein.
Eigenschaften
- Eine symmetrische Matrix ist immer eine quadratische Matrix ↗
- Eine symmetrische Matrix stimmt überein mit ihrer transponierte Matrix ↗
- Eine symmetrische Matrix mit nur reellen Einträgen hat nur reelle Eigenwerte (externer Link)
- Eine symmetrische Matrix mit nur reellen Einträgen hat nur zueinander orthogonale Eigenvektoren ↗
- Symmetrische Matrix plus symmetrische Matrix = symmetrische Matrix
- Symmetrische Matrix mal symmetrische Matrix = symmetrische Matrix wenn AB=BA
- Symmetrische Matrix mal ihrer Transponierten = symmetrische Matrix
- Symmetrische Matrix mal Zahl = symmetrische Matrix
- Immer symmetrisch ist eine Diagonalmatrix ↗
- Immer symmetrisch ist die Nullmatrix ↗
- Immer symmetrisch ist die Einheitsmatrix ↗
Geometrische Deutung
- Die geometrische Wirkung einer symmetrischen Matrix ist reine Skalierung entlang orthogonaler Richtungen (den Eigenvektoren), kombiniert mit einer Drehung (Rotation), um diese Achsen auszurichten.
- Die Eigenvektoren zeigen die Hauptachsen der Transformation.
- Die Eigenwerte bestimmen, wie stark in Richtung der Eigenvektoren gestreckt oder gestaucht wird.
- Symmetrische Matrizen beschreiben reine Skalierungen und Spiegelungen, keine Drehungen (außer triviale Drehungen um 180° bei negativen Eigenwerten).
- Keine Verzerrung der Winkel zwischen Eigenvektoren. Da die Eigenvektoren orthogonal bleiben, bleibt das Koordinatengitter entlang dieser Richtungen „rechtwinklig“ gestreckt.
Beispiel
Betrachten wir ein Quadrat in einem 2D-Koordinatensystem mit x- und y-Achse. Die linke untere Ecke des Qudarats soll im Koordinatenursprung liegen. Die Kantenlänge des Quadrats sei 4. Die vier Eckpunkte des Quadrats kann man dann als die Spitzen von vier Ortsvektoren auffassen. Die Spaltenvektoren sind hier horizontal geschrieben. Das hochgestellte groß T steht für das Wort "transponiert" und heißt, dass die Zeile als Spalte gedacht werden soll:
Quadrat
- Links oben: (0 4)ᵀ
- Links unten: (0 0)ᵀ
- Rechts unten: (4 0)ᵀ
- Rechts oben: (4 4)ᵀ
Matrix
5 2
2 2
Die Matrix symmetrische Matrix hat hier als obere Zeile die Einträge 5 und 2. Die untere Zeile hat die Einträge 2 und 2. Bei der Rechner Matrix mal Spaltenvektor kommt am Ende immer auch wieder ein Spaltenvektor heraus. Um eine solche Matrix wie oben angegeben mit einem Spaltenvektor wie z. B. (4 0)ᵀ zu multiplizieren, legt man die Einträge des Vektors gedanklich erst über die obere Zeile der Matrix. Zahlen, die dann übereinander liegen, werden multipliziert. Die zwei so entstehenden Produkte dann addiert. Dann geht man genauso für die zweite Zeile der Matrix vor. Für den Vektor (4 0)ᵀ rechnet man für die obere Zeile also: 5·4+2·0 = 20. Das ist die obere Zeile des Ergebnisvektors. Für die Zeile unten rechnet man 2·4+2·0 und erhält 8 als Eintrag für die untere Zeile des Ergebnisvektors. Eine ausführliche Rechenanleitung steht unter Matrix mal Vektor ↗
Transformiert
- Links oben: (8 8)ᵀ
- Links unten: (0 0)ᵀ
- Rechts unten: (20 8)ᵀ
- Rechts oben: (28 16)ᵀ
Trägt man die vier Eckpunkte des so mit der symmetrischen Matix transformierten ursprüngliches Quadrats ein, erkennt man ein Parallelogramm.
Eigenwerte
Die Eigenwerte λ einer 2x2-Matrix berechnet man, indem man zunächst als Unbekannte das Lambda λ von jedem Eintrag der Hauptdiagonalen abzieht.
5-λ 2
2 2-λ
Dann rechnet man die Determinante der Matrix aus: die Determinante einer 2x2-Matrix ist das Produkt der Hauptdiagonalen (links oben nach rechts unten) minus das Produkt der Einträge der Nebendiagonalen (links unten nach rechts oben). Der entsprechende Term wird dan gleich 0 gesetzt und die so entstandene quadratische Gleichung löst:
- (5-λ)(2-λ)-2·2 = 0 | Vereinfachen
- λ²-7λ+6 = 0 | pq-Formel ↗
- λ₁ = 6
- λ₂ = 1
Eigenvektoren
Die Eigenvektoren zur gegebenen Matrix berechnet man über die sogenannte Eigenvektorgleichung Av=λv, wobei A die gegebene Matrix und v für die gesuchten Eigenvektoren gehört. Man formt das um und erhält dann: (A-λ𝟙)·v = 0. Das Zeichen 𝟙 steht für die Einheitsmatrix. Schreibt man v als Vektor mit einer x- und einer y-Koordinate aus, erhält man für jeden Eigenwert je ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten:
- Vektor für λ₁ = 6: (2 1)ᵀ
- Vektor für λ₂ = 1: (-1 2)ᵀ
Diese Eigenvektoren müssen noch normiert werden. Normieren heißt für Vektoren, dass ihre Länge am Ende 1 betragen soll, ohne dass sie dabei aber die Richtung ändern. Siehe dazu mehr unter Vektor normieren ↗
- Normierter Vektor für λ₁ = 6: (+2/√5 +1/√5)ᵀ
- Normierter Vektor für λ₂ = 1: (-1/√5 +2/√5)ᵀ
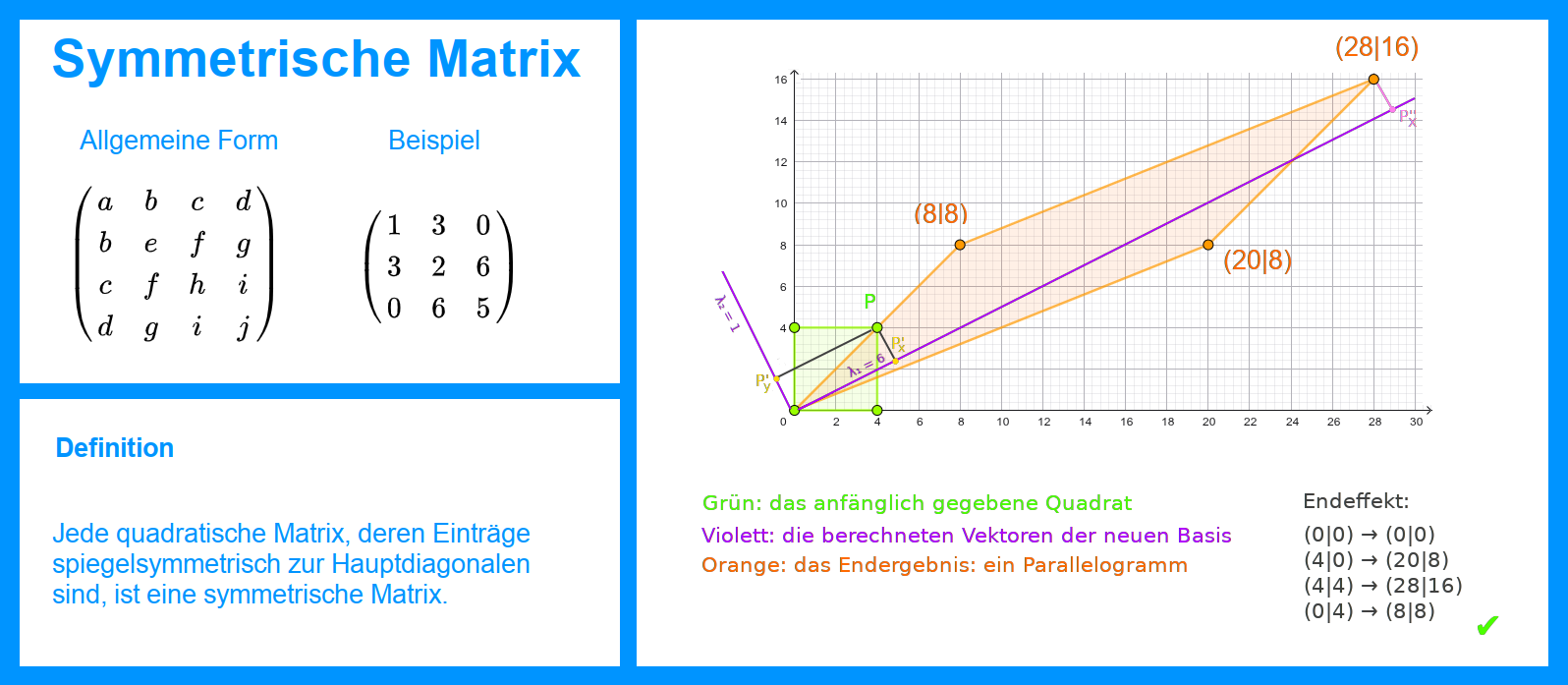
Interessant zur Deutung der gesamten Transformation ist es jetzt, die Eigenvektoren vom Koordinatenursprung aus gesehen ins vorhandene Koordinatensystem mit dem Quadrat und dem Parallelogramm einzutragen. Man erkennt dann die geometrische Bedeutung der Eigenvektoren und der Eigenwerte. Für jeden einzelnen Punkt des ursprünglichen Quadrates kann man die folgenden Schritte ausführen, um am Ende das Parallogramm zu erhalten:
- Zeichne die neuen Eigenvektoren ausgehend vom alten Koordinatenursprung ein.
- Für das geometrische Verständnis ist die Länge dieser Vektoren nicht wichtig.
- Projiziere einen Punkt der urpsprünglichen Figur auf beide neue Achsen.
- Man hat dann sozusagen den x- und den y-Wert des Punktes im neuen Koordinatensystem.
- Dann multipliziert man diese beiden Werte mit den entsprechenden Streckungsfaktoren, den Eigenwerten.
- Dabei darauf achten, dass man jeweils den Eigenwert nimmt, der zur entprechenden Koordinatenachse gehört.
- Die berechneten Ergebnisse geben den x- und den y-Wert des neuen Bildpunktens im neuen Koordinatensystem.
Führt man diese Schritte der Reihe nach für alle Punkte einer anfänglich gegebenen Figur durch, entsteht dadurch eine neue Bildfigur. Die so durchgeführte Transformation verbindet die Rotation mit einer getrennt kontrollierbaren Streckung oder Stauchung in x- und in y-Richtung (des neuen Koordinatensystems).