Bildinfo

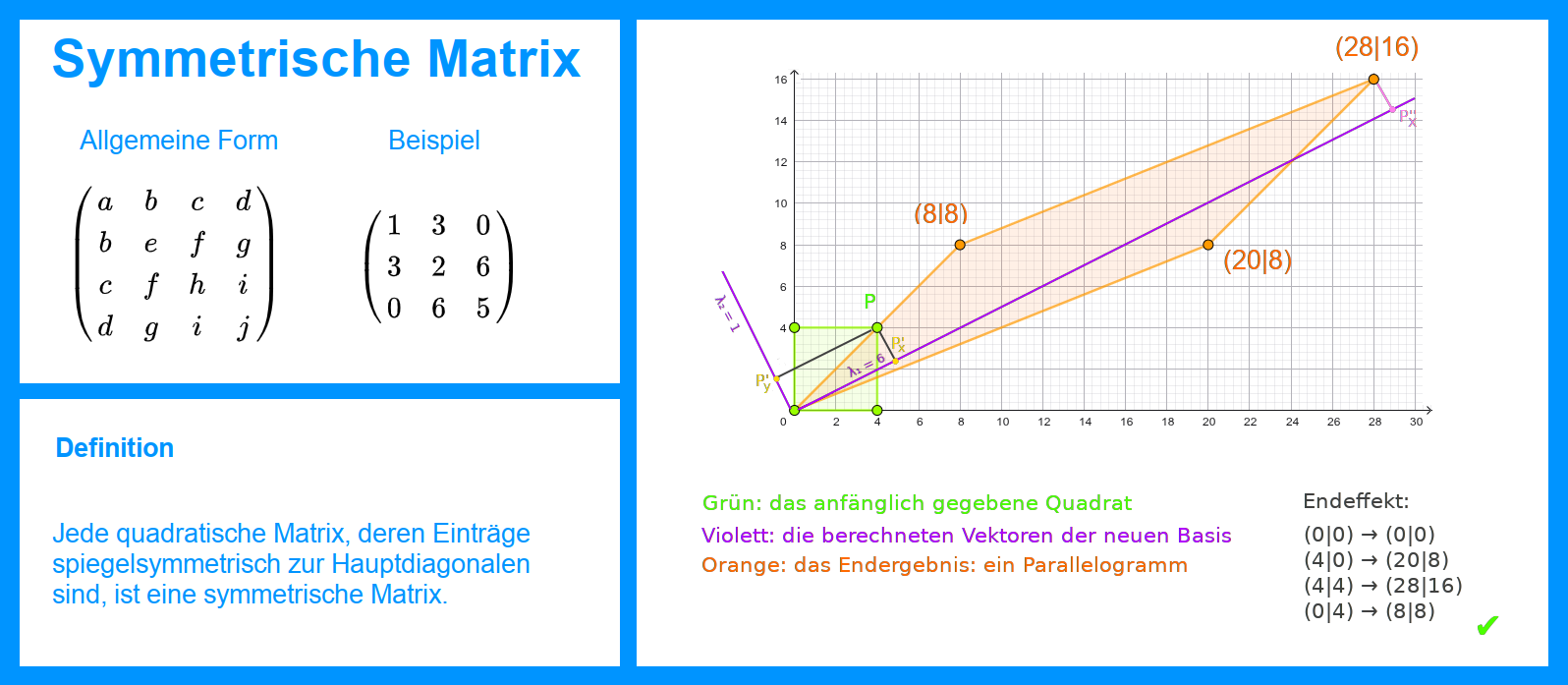
Anschaulich als Transformation oder Abbildung in einem 2D-Koordinatensystem: jeder Punkt einer anfänglichen Figur (hier das grüne Quadrat) wird einmal auf eine neue x-Achse und einmal auf eine neue y-Achse (beide hier violett) projiziert. Die x- und y-Werte der Projektionen werden dann mit den entprechenden Faktoren, vorgegeben durch die Eigenwert der Matrix, multipliziert. Sie geben die Koordinaten des neuen Bildpunktes im neuen Koordinatensystem. Für alle Punkte einer anfänglich gegebenen Figur entsteht so am Ende die rotierte und gestreckte beziehungsweise gestauchte neue Bildfigur.

Source

No guarantee can be given as to the correctness of facts implied or explicitly stated.