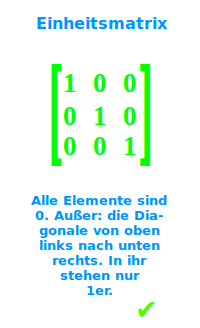
Einheitsmatrix
𝟙
© 2016
- 2025
Basiswissen|
Eigenschaften|
Sie ist immer quadratisch|
Einheitsmatrix als neutrales Element|
Synonyme
Basiswissen
Alle Elemente einer sogenannten Einheitsmatrix sind Nullen. Nur in der Hauptdiagonalen, die Diagonale von oben links nach unten rechts) stehen keine Nullen sondern ausschließlich nur Einsen als Einträge. Die Einheitsmatrix ist damit ein Sonderfall einer Diagonalmatrix. Eine übliche Abkürzung ist der lichte Buchstabe 𝟙, eine 1 mit doppelt geschriebenem senkrechten Strich.
Eigenschaften
- Eine Einheitsmatrix ist immer quadratisch.
- Sie besteht fast nur aus Nullen, außer ...
- Von links oben nach rechts unten geht eine Diagonale aus 1ern.
- Die Hauptdiagonale besteht also nur aus 1ern.
- Jede solche Matrix ist eine Einheitsmatrix.
Sie ist immer quadratisch
- Quadratisch bei Matrizen heißt: Anzahl Zeilen = Anzahl Spalten.
- Eine Einheitsmatrix hat also immer genauso viele Zeilen wie Spalten.
- Die kleinstmögliche Einheitsmatrix ist [1]: eine Zeile, eine Spalte.
- Siehe auch 👉 quadratische Matrix
Einheitsmatrix als neutrales Element
- Die Einheitsmatrix ist das neutrale Element der Matrizenmultiplikation.
- Irgendwas mal Einheitsmatrix gibt immer wieder das "Irgendwas".
- Mehr unter 👉 Matrix mal Matrix