Definition

Als Diagonalmatrix bezeichnet man eine Matrix, bei der alle Einträge außerhalb der Hauptdiagonalen Null sind. Die Hauptdiagonale geht von oben links nach unten rechts.

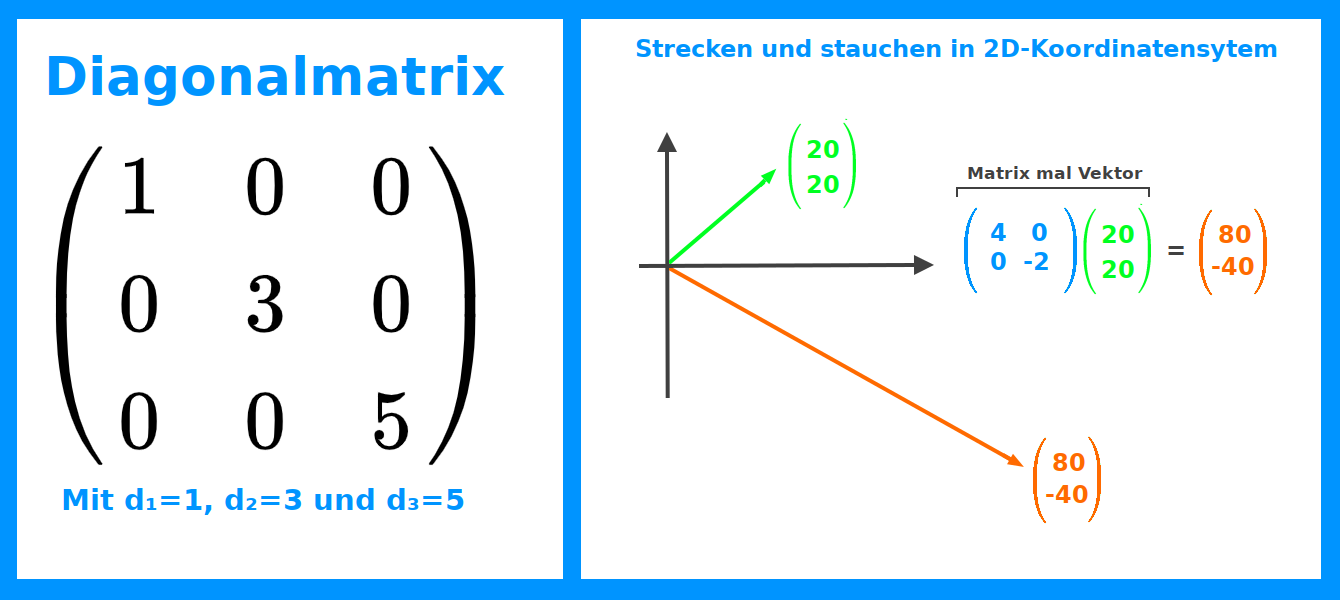
Bildbeschreibung und Urheberrecht — Mit einer Diagonalmatrix kann man rechnerisch recht leicht Objekte nach unterschiedlichen Faktoren entlang der verschiedenen Koordinatenachsen strecken und stauchen. © Kmhkmh (Wikimedia) ☛

Geometrische Wirkung

Wendet man in einem 2D-Koordinatensystem mit x- und y-Achse eine Diagonalmatrix auf einen Spaltenvektor an, im Sinne von Matrix mal Vektor, so kann der Vektor in x- und y-Richtung gestaucht und gestreckt werden. Eine Diagonalmatrix im 2D bewirkt auf einen Vektor eine Skalierung (Streckung oder Stauchung) entlang der Koordinatenachsen.

Allgemein

a 0
0 d

Gegeben ist die Matrix mit der Zeile a 0 oben und der Zeile 0 d unten.

Wird diese Diagonalmatrix auf einen Vektor v = (x, y) angewendet, ergibt sich der neue Vektor v' = (ax dy).

Wirkung

Skalierung der x-Koordinate: Die x-Koordinate wird mit dem Diagonalelement a multipliziert.

Skalierung der y-Koordinate: Die y-Koordinate wird mit dem Diagonalelement d multipliziert.

Wenn |a| > 1, wird der Vektor in x-Richtung gestreckt.

Wenn 0 < |a| < 1, wird der Vektor in x-Richtung gestaucht.

Wenn a oder d negativ ist, erfolgt zusätzlich eine Spiegelung an der entsprechenden Achse (d. h. an der y-Achse bei negativem a, an der x-Achse bei negativem d).

Es findet keine Rotation oder Scherung statt.

Beispiel

Wendet man die Matrix

+4 +0
+0 -2

Auf den Vektor Spaltenvektor (20 20)ᵀ an, so erhält man den neuen Spaltenvektor v'=(80 -40)ᵀ.^[1] Der ursprüngliche Vektor zeigte als Ortsvektor gedacht (Anfang liegt im Koordinatenursprung) vom Punkt (0 0) des Koordinatensystems diagonal nach oben rechts. Der transformierte Vektor (80 -40) hat nun eine doppelt so stark gestreckte x-Komponente im Vergleich zur y-Komponente. Der Vektor geht also wesentlicher weiter in x-Richtung als in y-Richtung. Zusätzlich wurde der Vektor bei der Transformation von v zu v' an der x-Achse gespiegelt: der y-Wert wurde vom Vorzeichen her geändert.

Fußnoten

[1] Das hochstellte große T steht für für die sogenannte transponierte Matrix. Das heißt, dass der hier im Fliextext als Zeilenvektor (20 20) geschriebene Vektor eigentlich als Spaltenvektor aufzufassen ist.