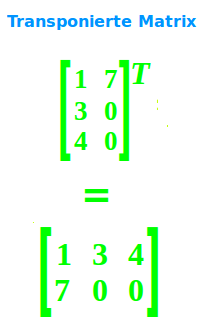Basiswissen

Eine transponierte^[1], gestürzte^[2] oder gespiegelte Matrix ist eine Matrix, bei der ausgehend von einer anderen Matrix die Spalten (oben nach unten) zu Zeilen (links nach rechts) gemcht wurden. Das wird hier kurz mit Beispieln erklärt.

Bildbeschreibung und Urheberrecht — Man sieht zwei grüne Matrizen.☛

Definition einer transponierten Matrix

Man hat eine Matrix gegeben.

Man nimmt davon die erste Spalte [oben nach unten] ↗

Diese gibt von der neuen Matrix die erste Zeile [links nach rechts] ↗

Die Zahlen die vorher weiter oben standen stehen in der transponierten Matrix weiter links.

Dann nimmt man von der alten Matrix die zweite Spalte…

und macht daraus von der neuen Matrix die zweite Zeile.

Und so weiter mit allen Spalten der alten Matrix.

Die neue Matrix ist dann die Transponierte der alten Matrix.

Formale Schreibweise

Aᵀᵢₖ = Aₖᵢ^{[1, Seite 10]}

Zahlenbeispiel

Die Matrix am Anfang des Beispiels besteht aus zwei Zeilen (von links nach rechts) und drei Spalten (von oben nach unten).

1 3 5
4 0 0

Man nimmt dann von links nach rechts jede einzelne Spalte und kippt sie gedanklich nach links um und macht sie so zu Spalten:

1 4
3 0
5 0

Zahlen, die in einer Spalte am Anfang weiter oben standen, stehen dann in der entsprechenden Zeile weiter links. Spalten die vorher weiter links standen, stehen nachher als Zeilen weiter oben.

Vektoren in Zeilenschreibweise

Die einzelnen Koordinaten eines Vektors, zum Beispiel als reelle Zahlen, schreibt man üblicherweise von oben nach unten in einer Spalte übereinander. Alternativ kann man den Vektor aber auch in Zeilenform schreiben. Eine Variante davon ist dann, dass man zum Beispiel mit dem hochgestellten großen T (für transponieren) deutlich macht, dass der Vektor eigentlich als Spalte geschrieben gedacht werden sollte:

(4 5 7)ᵀ

Man geht von links nach rechts alle "Spalten" des Vektors durch und macht sie durch umstürzen nach links gedanklich zu Zeilen. Aus der 4 wird so die erste Zeile, aus der 5 die zweite und aus der 7 die dritte Zeile. So entsteht aus (4 5 7)ᵀ durch Transponieren:

4
5
7

Links und rechts wird dieser Spaltenvektor noch durch runde Klammern eingeschlossen, die hier nicht dargestellt sind. Über das Transponieren kann man also aus einem Spaltenvektor einen Zeilenvektor machen, und umgekehrt. Siehe auch Zeilenvektor ↗

Fußnoten

[1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 2. 14. Auflage, 2019. ISBN: 978-3-658-07789-1. Verlag Springer Vieweg. Dort die Seite 10: Transponierte einer Matrix. Siehe auch Der Papula ↗

[2] Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Dort die Seite 277: transponierte oder gestürzte Matrizen. Siehe auch Der Bronstein ↗