Basiswissen

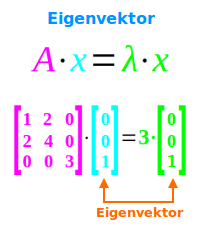
A·x = λ·x: eine Matrix A wird mit einem Vektor x multipliziert. Wenn man die Matrix A durch eine reelle Zahl λ ersetzen könnte, ohne dass sich dadurch der Ergebnisvektor ändert, dann ist λ ein Eigenwert der Matrix A und x ein Eigenvektor dieser Matrix.^[3]

Bildbeschreibung und Urheberrecht — Hat eine Matrix A einen Vektor x, der mit dieser Matrix multipliziert das gleiche Ergebnis ergibt, wie bei der Multiplikation mit einer reellen Zahl, dann ist dieser Vektor x ein Eigenvektor der Matrix A.☛

Formel

A·x = λ·x

Legende

A mal x Matrix mal Vektor ↗

λ mal x Zahl mal Vektor ↗

A ist eine beliebige quadratische Matrix ↗

x ist ein Vektor. Seine Höhe ist gleich der Breite von A.

λ steht für eine beliebige reelle Zahl

In Worten

In Worten heißt diese Gleichung: es gibt eine reelle Zahl λ, mit der man einen Vektor multiplizieren kann und zwar so, dass dabei dasselbe Ergebnis herauskommt, wie bei der Multiplikation der Matrix A mit dem Vektor.

Anschauliche Interpretation

Multipliziert man eine Matrix A mit einem ihrer Eigenvektoren x, dann ist das Ergebnis wieder ein Vektor. Dieser Vektor ist immer kollinear wie der Ausgangsvektor x. Kollinear heißt: parallel. Der Ergebnisvektor kann aber eine andere Länge und eine andere Orientierung haben als der Ausgangsvektor x.

Verallgemeinerung: komplexen Zahlen

Die bisherige Definition war beschränkt auf reelle Zahlen als λ-Werte. Aber sowohl die Elemene der Matrix als auch λ können auch für komplexe Zahlen definiert werden. Dieser Fall wird hier aber nicht weiter untersucht.

Hat jede Matrix Eigenvektoren?

Ja und nein: es kommt auf die betrachteten Zahlenbereiche an:

Jede reelle Matrix hat Eigenvektoren, wenn λ komplex sein darf.

Nicht jede reelle Matrix hat Eigenvektoren, wenn λ reell sein muss.

Was ist das Eigenwertproblem?

Man hat eine bestimmte Matrix gegeben.

Dazu sollen die möglichen Eigenwerte (und Eigenvektoren) gefunden werden.

Diese Rechnung kann sehr aufwändig werden

Der übliche Name ist Eigenwertproblem ↗

Fußnoten

[1] Revolution in der linearen Algebra. In: Spektrum der Wissenschaft 5.20 (Mai 2020). Der Artikel stellt eine vereinfachte Berechnungsmethode vor.

[2] Peter B. Denton, Stephen J. Parke, Terence Tao, Xining Zhang: Eigenvectors from eigenvalues: A survey of a basic identity in linear algebra. In: Bulletin of the American Mathematical Society. Published 2021. DOI: 10.1090/bull/1722

[3] "Zu einer Matrix A nennen wir v einen Eigenvektor und λ einen Eigenwert, wenn Av = λv erfüllt ist." In: Michaela Miedler: Mathematische Bausteine zum Erlernen des Formalismus der Quantentheorie. Diplomarbeit. Universität Wien. Fakultät für Physik. Betreut von Beatrix Hiesmayr. 2019. Online: https://utheses.univie.ac.at/detail/50004