Basiswissen

Reflexion heißt so viel wie Zurück-Beugung: eine Reflexion von Licht heißt, dass das Licht an irgendeiner Fläche abprallt und nicht etwa in diese Fläche eindringt oder durch sie hindurchgeht. Zunächst werden verschiedene Formen von Reflexion vorgestellt. Anschließend werden die wichtigsten physikalischen Prinzipien dazu erklärt.

Bildbeschreibung und Urheberrecht — Man sieht den Wiederschein einer Parklampe in eine Teich.☛

Verschiedene Formen von Reflexion

Betrachtet man das Auftreffen von Licht auf einen festen Körper oder eine Flüssigkeit, so wird unter bestimmten Umständen eine mehr oder minder großer Teil des auftreffenden Lichts von dem Körper nicht aufgenommen oder durchgelassen. Vielmehr wird das Licht zurück geworfen in das Medium, aus dem es kam.

Spiegelung: Einfallswinkel-gleich-Ausfallswinkel

Trifft Licht auf seinem Weg durch Luft, Wasser oder ein anderes durchsichtiges Medium auf eine große flache und glatte Fläche aus spiegelende Material, so wird ein großer Teil des Lichts wieder in das Ursprungsmedium zurückgeworfen. Dabei folgt das Licht dem Gesetz Einfallswinkel-gleich-Ausfallswinkel. Das gilt ganz gleich, ob man sich das Licht wellenhaft, aus Strahlen oder kleinen Teilchen vorstellt.

Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.

Das Reflexionsgesetz mit Lichtstrahlen. Die Winkel werden zum sogenannten Lot hin angegeben.

Eine Besonderheit in der mathematischen Beschreibung ist, dass man die Winkel nicht auf die spiegelnde Fläche bezieht, sondern auf eine Ebene oder Linie senkrecht dazu, das sogenannte Lot. Mir ist kein praktischer Grund dafür bekannt, möglicherweise hat es nur historische Gründe. Siehe mehr unter Einfallswinkel gleich Ausfallswinkel ↗

Partielle Reflexion

Trifft Licht auf glattes ebenes Glas, etwa von einem Fenster, so wird üblicherweise nur ein Teil davon reflektiert. Ein anderer Teil geht durch das Glas hindurch. Das kann man leicht selbst beobachten. Bei Dunkelheit betrachtet man von außen einen beleuchteten Raum. Man erkennt durch die Fensterscheibe hindurch alle Gegenstände im Inneren.

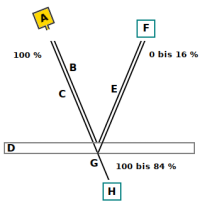
Eine Lichtquelle A sendet einen Strahl aus, den man sich aus zwei Teilen A und B vorstellen kann. Von einer Glasplatte D wird ein Teil des Strahls E reflektiert und von einem Detektor F gemessen. Ein anderer Teil G des Strahl geht durch die Glasplatte hindurch und erreicht den Detektor H.

Geht man dann ins Innere des Raumes, kann man an der Fensterscheibe ein Spiegelbild genau jener Gegenstände sehen. Ein Teil des Lichts musste als durch die Scheibe gegangen sein, ein anderer Teil wird an ihr reflektiert. Dieses nur teilweise Reflexion nennt man partielle Reflexion ↗

Totalreflexion

Trifft Licht relativ flach auf eine Grenzfläche, etwa von Wasser zu Luft, so wird es vollständig reflektiert. Das kann man leicht nachvollziehen, wenn man den Finger knapp unter die Wasseroberfläche hält. Blickt man zunächst senkrecht von oben nach unten auf den Finger, kann man ihn gut erkennen. Geht man dann mit den Augen aber immer näher an die Wasseroberfläche heran, so wird der Finger irgendwann in die Unsichtbarkeit verschwinden. Dieses Phänomen bezeichnet man als Totalreflexion ↗

Retroreflexion

Wird Licht von einer Fläche in exakt dieselbe Richtung zurückgeworfen, aus der es ursprünglich auch kam, so spricht man von einer Retroreflexion. Bauteile, die dazu in der Lage sind, werden meist künstlich hergestellt. Das klassische Beispiel sind Katzenaugen an Fahrrädern. Der Sinn ist, dass das Licht von Schweinwerfen nicht in irgendeine Richtung reflektiert wird sondern in die Richtung aus der es kam. So gelangt möglichst viel Licht in die Richtung anderer Radfahrer oder Autofahrer, was die Erkennbarkeit erhöht. Siehe mehr unter Retroreflexion ↗

Diffuse Reflexion

Licht kann nicht nur von glatten ebenen und spiegelnden Flächen reflektiert werden. Auch rauhe Oberflächen wie Papier, Blätter oder unruhiges Wasser reflektieren Licht. Das kann man leicht nachvollziehen, indem man bei Dunkelheit eine kleine schwache Kerze in einem Raum mit heller Tapete anzündet. Stellt man in eine Richtung ein Brett hinter die Kerze, so wird es dort keinen absoluten dunklen Schattenraum geben. Es wird dort eine Resthelligkeit geben, in der man noch mehr oder minder gut sehen kann. Das Licht dazu stammt von der Reflexion des Kerzenlichts an den Wänden des Raumes. Siehe mehr unter diffus ↗

Irisieren

Viele Insekten haben wunderschön bunt schillernde Teile an ihrem Körper. Dasselbe gilt auch für viele Federn von Vögeln. Je nachdem von welcher Richtung aus man auf die Tiere blickt, erscheinen sie in anderen Farben. Der Grund dafür ist, dass verschiedene Farben des Lichts in unterschiedliche Richtungen reflektiert werden. Man bezeichnet den Effekt als Irisieren ↗

Die Physik der Reflexion von Licht

Wie die Reflexion von Licht zustande kommt wird durch unterschiedliche Modelle beschrieben. Bis auf eine Ausnahme kann kein Modell alle Phänomene der Optik erklären.

MERKSATZ:

1.0 Es gibt "gute falsche" und "richtige aber unpraktische Modelle".

Ein Modell kann falsch sein, aber es ist gut, wenn es auf einfache Weise praktisch nützliche Vorhersagen machen kann. Das klassische Beispiel dafür ist das Strahlenmodell der Optik. Umgekehrt kann ein richtiges Modell für viele Fälle unpraktisch sein. Das für die gesamte Optik zutreffende Modell scheint die Quantenelektrodynamik zu. Ihre Grundzüge sind zwar vergleichsweise leicht zu verstehen.^[1] Doch jede praktisch nutzbare Anwendung erfordert eine Mathematik zu der nur wenige Menschen in der Lage sind. Es werden nun einzelne Modelle für die Reflexion von Licht vorgestellt.

Die Lichtreflexion in der Strahlenoptik

In der sogenannten Strahlenoptik stellt man sich Licht als gerade Strahlen vor, die aus einer Lichtquelle austreten. Treffen die Strahlen auf ein Hindernis, so werden sie auf eine mehr oder minder mechanisch gedachte Weise wie eine Kugel an einer flachen Ebene reflektiert. Es gilt das Gesetz Einfallswinkel-gleich-Ausfallswinkel. Mit diesem Modell kann man viele Strahlengänge in optischen Geräten und viele Effekte rund um echte Spiegel für viele praktische Zwecke ausreichend gut beschreiben und berechnen.

MERKSATZ:

2.0 Das Strahlenmodell ist sehr einfach zu verstehen und anzuwenden. Es ist für viele praktische Probleme die erste Wahl.

Dringt man aber gedanklich und experimentell in die Welt der mikroskopisch oder der submikroskopisch gedachten Materie ein, wird es schwierig. Spätestens wenn man in Atomen und Molekülen denkt, ist keine Oberfläche mehr wirklich glatt und eben. Jede Oberfläche muss dann als gewellt, gezackt oder sonstwie unregelmäßig gedacht werden. Denkt man sich die Strahlen des Lichts dann als sehr dünn im Vergleich zu diesen Strukturen, müssten sie an jeder so gedachten Oberfläche unregelmäßig in ständig andere Richtungen reflektiert werden. Damit dürfte es in der Wirklichkeit auch keine wirklich gut spiegelnden Flächen geben. Dass es aber solche Flächen doch gibt, ist ein Hinweis darauf, dass das Strahlenmodell des Lichts spätestens im Bereich mikroskopisch kleinen Materie versagt. Siehe mehr dazu unter Strahlenoptik ↗

Die Lichtreflexion in der Wellenoptik

In der Schulphysik der höheren Klassen wird nach dem Strahlenmodell des Lichts oft die sogenannte Wellenoptik behandelt. Das Licht wird dann als eine Erscheinungsform hypothetischer Wellen gedacht, die sich im Raum fortfplanzen. Zur Erklärung verschiedener Phänomen, etwa auch der Reflexion, dient dann das sogenannte Huygenssche Prinzip: an jeder Stelle einer Wellenfront entsteht eine neue Welle. Siehe auch Huygenssches Prinzip ↗

MERKSATZ:

3.0 Die Wellenoptik kann fast alle Phänomene der Optik erklären. Sie ist mathematisch anspruchsvoller als die Strahlenoptik. Sie umfasst auch die sogenannten Materiewellen.

Mit diesem Modell lässt sich nicht nur die Reflexion von Licht an Grenzflächen erlären, sondern auch Phänomene, die die Strahlenoptik überhaupt nicht erklären kann. Das sind vor allem Beugung und Interferenz. Dennoch ist auch das Huygenssche Prinzip beschränkt. Es kann nicht erklären, wie es zu einer partiellen Reflexion von Licht kommt, speziell dann, wenn ein dickeres Glas weniger Licht reflektiert als ein ansonsten gleiches nur dünneres Glas. Siehe auch Wellenoptik ↗

Die Lichtreflexion in der Quantenelektrodynamik

Das einzige Modell, dass die Reflexion von Licht rundum korrekt beschreibt ist die sogenannte Quantenelektrodynamik, kurz QED.^[1] Ob mit Wellen gedacht oder ganz ohne mit den sogenannten Quantenpfaden: dieses Modell ist selbst für einfachste Begebenheiten mathematisch so aufwändig, dass es selbst für viele Physiker praktisch nicht anwendbar ist und bei sehr komplexen Systemen wahrscheinlich gilt, aber noch nicht bewiesen ist.^[2]

Der Physiker und Nobelpreisträger Richard Feynman (1918 bis 1988) aber besteht darauf, dass die grundlegenden Gedanken von jedem gebildeten Laien gut nachvollzogen werden können. Feynman hat das ausführlich und ganz ohne Mathematik in einem eigenen Buch dargelegt.^[1]

MERKSATZ:

4.0 Das fundamentalste und damit "richtigste" Modell ist die Quantenelektrodynamik. Aber schon einfachste Anwendungen wie ein Strahlengang durch verschiedene Linsen erfordern eine Mathematik, zu der nur sehr wenige Menschen in der Lage sind.

Es sind vor allem zwei sehr überraschende Effekte im Zusammenhang mit der Reflexion von Licht, die nur die Quantenelektrodynamik richtig erklärt.

a) Richtet man einen Strahl Licht schräg von Luft kommenden auf eine ebene Fläche Glas, so geht ein Teil des Lichts durch das Glas hindurch, ein anderer Teil wird von dem Glas reflektiert. So weit so gut. Merkwürdige ist nun, dass man das Glas dicker machen kann und dann zunächst mehr Licht reflektiert wird. Macht man das Glas aber wiederum noch einmal dicker, so wird wieder weniger Licht reflektiert. Es scheint so zu sein, dass der Lichtstrahl nicht nur mit der Oberfläche wechselwirkt. Vielmehr scheint sein Verhalten bei der Reflexion durch die Information über die gesamte Dicke des Glases beeinflusst zu sein.

b) Ein zweites damit verwandtes Phänomen führt zur Idee eines Beugungsgitters. Feynman zeichnet einen Lichtstrahl, der an einer Stelle einer glatten Oberfläche, einem Spiegel etwa, nach dem Gesetz Einfallswinkel-gleich-Ausfallwinkel reflektiert wird. Dann sagt er, dass man in einiger Entfernung zum Berührungspunkt des Lichtstrahls mit dem Spiegel irgendwo den Spiegel etwas zerkratzen können. Darauf hin würde sich auch der Winkel der Reflexion ändern. Im Strahlenmodell erscheint die zerkratzte Stelle dabei weit ab des Weges des Strahles.

Fußnoten

[1] Richard Feynman: QED: Die seltsame Theorie des Lichts und der Materie. Piper Verlag. 1. Auflage 1992. ISBN: 3-492-21562-9. Siehe auch QED (Feynman) ↗

[2] Die QED ist sehr gut belegt, wenn es um Vorhersagen an Systemen mit wenigen Teilchen geht. Bei einer großen Anzahl - Millionen bis Trillionen oder darüberhinaus - ist die Theorie wahrscheinlich gültig, aber experimentell noch nicht bestätigt. Das betont der Physiker und Nobelpreisträger Richard Feynman (1918 bis 1988), wenn er schreibt: "Wenn ich behaupte, daß sich alle Phänomene der physikalischen Welt mit dieser Theorie erklären lassen, so nehme ich den Mund etwas voll, Bei den meisten uns vertrauten Erscheinungen ist eine so gewaltige Zahl Elektronen im Spiel, daß unser armer kleiner Verstand Mühe hat, dieser Vielfalt zu folgen. In solchen Situationen können wir mit Hilfe der Theorie ungefähr angeben, was passieren sollte und was dann unter diesen Umständen auch in etwa passiert. Stellen wir dagegen im Labor ein Experiment mit nur wenigen Elektronen unter einfachen Bedingungen zusammen, können wir mit großer Genauigkeit berechnen, was eintreten wird und können das mit ebenso großer Genauigkeit messen." In: Richard Feynman: QED: Die seltsame Theorie des Lichts und der Materie. Piper Verlag. 1. Auflage 1992. ISBN: 3-492-21562-9. Dort die Seite 18. Eine rechnerische Methode zum Umgang mit großen Anzahlen von Teilchen ist eine Simulation ↗