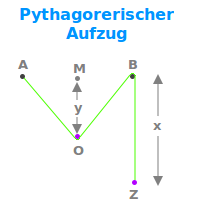
Pythagoreischer Aufzug
Mathematik
© 2016
- 2025
Basiswissen|
Pythagoreischer Aufzug (Erste Ableitung)|
Pythagoreischer Aufzug (zweidimensionale Funktion)|
Pythagoreischer Flaschenzug (zweidimensionale Funktion)|
Der pythagoreische Aufzug als Spiralcurriculum|
Fußnoten
Basiswissen
Als pythagoreischen Aufzug oder auch als pythagoreischen Flaschenzug, bezeichnen wir irgendeine einfache Anordnungen aus Haken, Seilen und Gewichten, gegebenenfalls auch Rollen, mit denen mathematische Funktionen geometrisch-anschaulich untersucht werden können. In irgendeiner Form spielt dabei auch der Satz des Pythagoras eine Rolle.

Verschiedene Versionen des pythagoreischen Aufzugs
Pythagoreischer Aufzug (Erste Ableitung)
y=f(x): eine sehr einfache Anordnung, die in kurzer Zeit mit zum Beispiel Reißzwecken und einem Faden auf einem Stück Pappe aufgebaut werden kann. Folgende Themen lassen sich mit dem Versuch gut anschaulich untersuchen:
f(x) ↗
Abhängige Variable ↗
Unabhängige Variable ↗
Ableitung über Kettenregel ↗
Erste Ableitung anschaulich ↗
An Vorkenntnissen hilfreich ist es, wenn man sicher mit der Kettenregel ableiten kann und den Satz des Pythagoras kennt. Siehe mehr pythagoreischer Aufzug (erste Ableitung) ↗
Pythagoreischer Aufzug (zweidimensionale Funktion)
z=f(x;y): eine Funktion bei der man zwei Variablen als Input, also sogenannte Funktionsargumente hat und einen Wert als Ergebnis, Output oder Funktionswert nennt man zweidimensional. Zweidimensionale Funktionen spielen in der höheren Mathematik und bei vielen Awendungen etwa in der Physik, den Ingenieur- und Wirtschaftswissenschaften eine wichtige Rolle. Mit wenig Haushaltsmaterial und in einigen Minuten ist ein einfacher Versuch aufgebaut, der direkt zu anspruchsvollen Themen wie partielle und totale Ableitung, Kurvenscharen und 3D-Graphen führt. Siehe dazu die Beschreibung des Versuchs unter pythagoreischer Aufzug (zweidimensionale Funktion) ↗
Pythagoreischer Flaschenzug (zweidimensionale Funktion)
z=f(x;y): ähnlich wie der pythagoreische Aufzug für eine zweidimensionale Funktion, nur etwas komplizierter. Durch den Flaschenzug-Effekt sind die mathematischen Beziehung schwieriger. Der Versuch kann mit Reißzwecken, Pappe, Seilen und einem Rollenblock oder alternativ auch mit Magnethaken an einer Tafel aufgebaut werden. In beiden Fällen ist der Gedanke, dass der Input, also das Argument, der Funktion ein Paar aus einem x- und einem y-Wert ist. Der Output oder der Funktionswert z hängt dann über eine Formel von diesem Input ab:
Abhängige Variable ↗
Unabhängige Variable ↗
Zweidimensionale Funktion ↗
3D-Graph ↗
Ableitung über Kettenregel ↗
Erste Ableitung anschaulich ↗
Partielle Ableitung ↗
Totale Ableitung ↗
Um die mathematischen Zusammenhänge zu verstehen, kann man sich mehrere Stunden mit der Versuchsanordnung beschäftigen. Die funktionalen Zusammenhänge sind nicht gegeben. Sie müssen erst selbst erstellt werden. Siehe mehr unter Pythagoreischer Flaschenzug (zweidimensionale Funktion) ↗
Der pythagoreische Aufzug als Spiralcurriculum
Von einem Spiralcurriculum spricht man, wenn ein und dieselbe Betrachtung, ein und derselbe Versuch über mehrere (Schul)Jahre hinweg immer wieder neu betrachtet werden kann, und sich dabei jedes mal dem Alter oder dem Lernstand entsprechen neue Aspekte behandeln lassen.[2] Zum pythagoreischen Aufzug, in irgendeiner seiner Versionen, stehen hier kurz einige Vorschläge.
- Grundschule: mechanisch einfache Version. Man darf das lose Ende L zum Beispiel nur senkrecht oder waagrecht bewegen und fasst Zahlenverbindungen in Worte: wenn ich das Seil rechts nach unten zieht, geht das Gewicht nach oben. Oder: wenn ich Seil vier Schritte nach rechts ziehe, geht das Gewicht vier Schritte nach oben.
- Klasse 5: man erstellt aus einer einfachen Anordnug eine Wertetabelle.
- Klasse 6: man denkt sich dazu einfache Textaufgaben zum praktischen Lösen aus.
- Klasse 7: man baut den Versuch so auf, dass der Wert von z eine proportionale Funktion x ist.
- Klasse 8: man baut den Versuch so auf, dass der Wert von z eine lineare Funktion von x ist
- Klasse 9: man bringt irgendwie den Satz des Pythagoras mit hinein. Formel suchen?
- Klasse 10: man beschäftigt sich mit dem Definitions- und Wertebereich
- Klasse 11: man bringt die Idee der ersten Ableitung mit hinein.
- Studium: zweidimensionale Funktion, Skalarfeld, partielle Ableitung, Nabla-Operator, Gradient, Vektorfeld, Vektoranalysis
Man kann den Grad der Schwierigkeiten vor allem dadurch verändern, dass man auf der rechten Seite entweder Bewegungen nur in x- oder nur in y-Richtung oder frei wählbar in beide Richtungen zulässt. Siehe mehr unter Spiralcurriculum ↗
Fußnoten
- [1] Dem Deutschen Wörterbuch der Deutschen Sprache (DWDS) zufolge (Stand 2024) ist pythagoreisch das korrektive Adjektiv zu Pythagoras. In: der Artikel "pythagoreisch". Siehe zum Beispiel auch pythagoreisches Tripel ↗
- [2] Siehe mehr unter Spiralcurriculum ↗