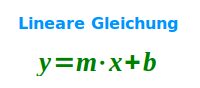Basiswissen

Allgemeine Definition

• y = mx + b
  

Legende

• y kann eine feste Zahl oder auch eine Unbekannte sein.
  

• m ist immer eine feste Zahl, jede Zahl ist erlaubt außer der 0.
  

• x ist immer eine Unbekannte und meist als Lösung gesucht.
  

• b ist immer eine feste Zahl, jede Zahl ist erlaub, auch die 0.
  

Definition in Worten

• In der Gleichung muss mindestens eine Unbekannte stehen.
  

• Die Unbekannte heißt meistens x, darf aber auch anders heißen.
  

• Das x darf mit jeder beliebigen Zahl malgenommen sein.
  

• Das x darf durch jede beliebige Zahl geteilt werden.
  

• Das x darf nicht mit Sinus, Wurzel etc. verbunden sein.
  

• Das x darf keine Hochzahl haben, x² oder x³ wären nicht erlaubt.
  

• Das x steht nie im Nenner (unten) von einem Bruch.
  

Mehrere Unbekannte

• Es darf beliebig viele Unbekannte geben.
  

• Häufig ist es, dass es x und y als Unbekannte gibt.
  

• Beispiel: y=4x+3. Das ist auch eine lineare Gleichung.
  

• So etwas heißt auch Geradengleichung ↗
  

Beispiele

• 16 = 4x + 2
  

• 4x + 2x = 20
  

• 3x = 9
  

Gegenbeispiele

• sin(x) + x = 4x - 8
  

• 8 = Wurzel von x
  

• 14 = 1/x
  

• x² = 25
  

Unlösbar

• Es gibt lineare Gleichungen, die nicht lösbar sind.
  

• Siehe als Beispiel x=x+1 ↗
  

Aufgaben

• Grundwertaufgaben [Fixkosten etc.]=> qck ↗
  

• Lineare Gleichung aus Minitexten => qck ↗
  

• Lineare Gleichungen lösen => qck ↗
  

Fußnoten

• [1] Zur Definition einer linearen Gleichung: "Eine Gleichung der Form , bx+c = 0, wobei b und c reelle Zahlen mit b ≠ 0 sind und x die gesuchte reelle Unbekannte ist, heißt lineare Gleichung. Die Unbekannte wird synonym auch als Variable bezeichnet. Die konstanten reellen Zahlen und nennt man Koeffizienten." In: HM4Mint NRW (höhere Mathematik für die MINT-Fächer in Nordrhein-Westfalen). Online-Kurs der integral-learning GmbH. Digitial Education Lab - IHK Berlin. Abgerufen am 26. Februar 2026. Online: https://hm4mint.nrw/hm1/link/HoeherMathem1/Teil1Grundl/1Rechen/LoesenElemenGleichGleich