Kathete über Tangens
Berechnung
© 2016
- 2025
Basiswissen
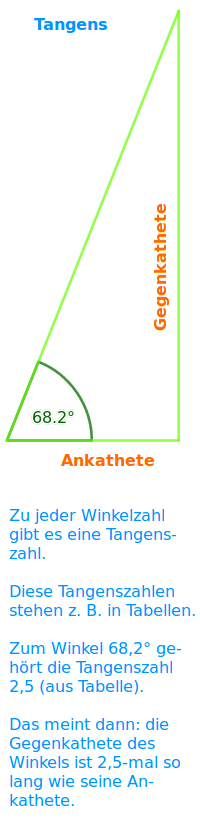
Katheten gibt es nur in rechtwinkligen Dreiecken. In einem rechtwinkligen Dreieck gibt es immer genau zwei Katheten: es sind die zwei kürzeren Seiten im Dreieck. Sie liegen immer direkt am rechten Winkel (90°-Winkel). Es wird gezeigt, wie man ihre Länge mit dem Tangens berechnen kann.
Was muss gegeben sein?
- Es muss immer die Länge von einer der zwei Katheten bekannt sein.
- Es muss immer einer der zwei nicht-90°-Grad Winkel bekannt sein.
- Damit kann man immer die Länge der anderen Kathete berechnen
Gegenkathete berechnen
- In dem Dreieck gibt es einen 90°-Grad Winkel.
- Es muss mindestens einer der beiden anderen Winkel bekannt sein.
- Es gibt eine Kathete, die direkt an diesem Winkel liegt.
- Diese Kathete an dem Winkel ist die sogenannte Ankathete.
- Man nimmt den Tangens von dem Winkel (Tabelle, Taschenrechner).
- Man multipliziert dieses Ergebnis mit der Länge der Ankathete.
- Das Endergebnis ist die Länge der Gegenkathete.
- Siehe auch 👉 Gegenkathete über Tangens
Ankathete berechnen
- In dem Dreieck gibt es einen 90°-Grad Winkel.
- Es muss mindestens einer der beiden anderen Winkel bekannt sein.
- Es gibt eine Kathete, die gegenüber von diesem Winkel liegt.
- Diese Kathete gegenüber des Winkels ist die sogenannte Gegenkathete.
- Man nimmt den Tangens von dem Winkel (Tabelle, Taschenrechner).
- Man dividiert die Länge der Gegenkathete durch diesen Winkel.
- Das Endergebnis ist die Länge der Ankathete.
- Siehe auch 👉 Ankathete über Tangens