Grundidee

Anleitung

• Man setzt zunächst jedes x im Funktionsterm in eine eigene Klammer.
  

• Die x'se im Funktionsterm nennt man auch das Funktionsargument ↗
  

• Man multipliziert dann jedes dieser eingeklammerten x'se mit -1.
  

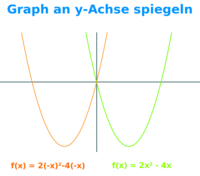
• Beispiel: f(x) = 2x²-4x ⭢ spiegeln ⭢ f(x) = 2·(-1·x)²-4·(-1·x)
  

• Klammern auflösen gibt: f(x) = 2x² + 4x
  

Tipps zur Rechnung

• Die Funktionsgleichung muss die Form "f(x) = Term" haben
  

• Alles rechts vom Gleichheitszeichen zusammen ist dann der Funktionsterm ↗
  

• Man muss alle x'se mit der Zahl minus Eins multiplzieren.
  

• Aus einem eingeklammerten (x) wird dann ⭢ (x·(-1))
  

• x·(-1) ist aber dasselbe wie -1·x oder kurz: -x
  

• Aus (x·(-1)) wird also immer: (-x)
  

• Dann löst man die Klammern auf:
  

• Aus (-x)² wird dann ⭢ x²
  

• Aus 2·(-x) wird ⭢ -2x
  

• Aus -2(-x) wird ⭢ +2x
  

• Siehe auch mal minus ↗
  

Die Spiegelung als Umklappen

• Durch die Spiegel an der y-Achse passieren folgende Änderungen:
  

• Punkte die vorher auf der y-Achse lagen ändern ihre Lage nicht.
  

• Punkte die vorher links von der y-Achse lagen, liegen dann rechts von ihr.
  

• Sie sind dann nach rechts genauso weit von der Achse entfernt, ...
  

• wie sie vorher links von der Achse von dieser entfernt waren.
  

• Punkte die vorher rechts von der y-Achse lagen, liegen dann links von ihr.
  

• Sie sind dann nach links genauso weit von der Achse entfernt, ...
  

• wie sie vorher vorher rechts von der Achse von dieser entfernt waren.
  

• Beispiele: der Punkt (0|4) bleibt der Punkt (0|4)
  

• Der Punkt (4|2) wird zum Punkt (-4|2)
  

• Der Punkt (-3|3) wird zum Punkt (3|3)
  

Die Spiegelung als Drehung

• Es gibt eine alternative Deutung der Spiegelung an der y-Achse.
  

• Sie führt zum selben Ergebnis wie die Deutung oben als Umklappen.
  

• Man stellt sich das Koordinatensystem mit einer fest y-Achse vor.
  

• Die gesamte Zeichenfläche und die y-Achse sind dann auf Glas gezeichnet.
  

• Diese gläserne Zeichenfläche kann um die y-Achse gedreht werden.
  

• Durch die Spiegelung wird sie um 180° um die y-Achse gedreht.
  

• Die x-Achse soll aber auch nach der Drehung weiter nach rechts zeigen.
  

• Diese gedachte Transformation ist identisch mit dem Umklappen von oben.
  

Weitere Transformationen

• Von oben nach unten umklappen heißt Graph an x-Achse spiegeln ↗
  

• Zum drehen, stauchen und strecken siehe Graphen transformieren ↗