A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Matrix

Mathematik

© 2016 - 2025


Basiswissen｜ Definition｜ Was ist die korrekte Mehrzahl?｜ Etymologie von Matrix｜ Matrix (Film)｜ Geologie｜ Fußnoten


Basiswissen


Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen[1], so als sei die ganze Matrix eine Zahl.



Bildbeschreibung und Urheberrecht
Man sieht zwei Schemata von Matrizen. © WissensDürster (on Wikimedia Commons) Ralf Pfeifer (on Wikimedia Commons) Gunter Heim ☛


Definition


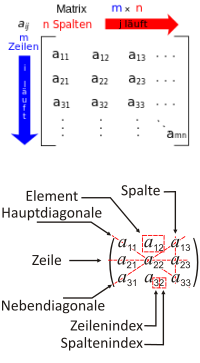
  • Eine Matrix besteht aus einzelnen Elementen (meistens Zahlen).
  • Die Elemente sind in Zeilen und Spalten angeordnet.
  • Um ein Element zu benennen gibt man erst die Zeile, dann die Spalte an.[2]
  • Matrizen benennt man mit Großbuchstaben, etwa A oder B.[3]

Was ist die korrekte Mehrzahl?


  • In der Mathematik gibt es Matrizen.
  • Die Einzahl in der Mathematik ist Matrix.
  • Die Einzahl ist nicht "Matrize".
  • Eine Matrize meint etwas anderes.

Etymologie von Matrix


Das Wort Matrix heißt im ursprünglichen altgriechischen Sinn so viel wie Muttertier. Es geht auf eine indoeuropäische Wurzel zurück und ist mit ähnlich lautenden Worten für Mutter aus Sprachen wie etwa dem Sanskrit (Indien), dem Persischen, Lateinischen, Englischen und Deutschen verwandt. Auch der physikalische Begriff der Materie ist sinngemäß damit verwandt, Materie nämlich als Mutter- oder Urstoff des Seienden. Siehe dazu auch unter Materie ↗

Matrix (Film)


Der US-amerikanische Film Matrix aus dem Jahr 1999 spielt in einer dystopischen Zukunft. Maschinen haben die Menschheit versklavt, nur eine kleine elitäre Minderheit durchblickt den Betrug und widersetzt sich dem Diktat der Maschinen. Siehe dazu Matrix (Film) ↗

Geologie


In der Geologie ist eine Matrix eine Art von feinkörnigem Kitt, der andere größere Gesteinsbrocken zusammen gekitet hat. Man spricht auch von einer Zementationen. Eine solche Matrix ist typisch für sogenannte Trümmergesteine, auch klastische Sedimente genannt. Typische Beispiele sind die Konglomerate mit rundlichen Brocken und die Brekzien mit den eckig-kantigen Brocken in der Matrix. Siehe als Beispiel auch Brekzie ↗

Fußnoten


  • [1] "MATRIX; A many-DIMENSIONal arrangement of numbers suitable to various TRANSFORMATIONs which form the basis of matrix algebra. A one-dimensional matrix is called a scalar. Most frequent are two-dimensional, n-by-m, matrices which might contain the coefficients (-> PARAMETER) of a set of LINEAR equations or specify a mapping" In: Klaus Krippendorf: A Dictionary of Cybernetics. Annaberg School of Economics. University of Pennsylvania. 1986. Online: https://asc-cybernetics.org/publications/Krippendorff/A_Dictionary_of_Cybernetics.pdf
  • [2] "Generell gilt für die Angabe des Formats Z × S, wobei Z die Anzahl der Zeilen und S die Anzahl der Spalten angibt." Und als Beispiel: "eine Matrix im Format 2 × 3 […] hat zwei Zeilen und drei Spalten". In: Michaela Miedler: Mathematische Bausteine zum Erlernen des Formalismus der Quantentheorie. Diplomarbeit. Universität Wien. Fakultät für Physik. Betreut von Beatrix Hiesmayr. 2019. Online: https://utheses.univie.ac.at/detail/50004
  • [3] "Matrizen werden mit Großbuchstaben bezeichnet und ihre Elemente mit entsprechenden Kleinbuchstaben. Die Indizies geben die Zeilen- und Spaltennummern an. Das Element a₁₂ ist in der Matrix A das Element der ersten Zeile und zweiten Spalte." Michaela Miedler: Mathematische Bausteine zum Erlernen des Formalismus der Quantentheorie. Diplomarbeit. Universität Wien. Fakultät für Physik. Betreut von Beatrix Hiesmayr. 2019. Online: https://utheses.univie.ac.at/detail/50004