A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

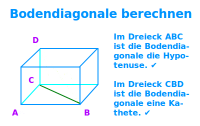
Bodendiagonale berechnen

Methoden

© 2016 - 2025


Basiswissen｜ Bodendiagonale über Pythagoras｜ Bodendiagonale über Trigonometrie


Basiswissen


Über Pythagoras oder Sinus/Cosinus: man hat eine quader-oder würfelförmige Kiste. Die Kantenlängen sind alle gegeben. Gesucht ist die Länge der Bodendiagonalen. Hier stehen kurze Anleitungen dazu.



Bildbeschreibung und Urheberrecht
Die Bodendiagonale ist Teil von zwei rechtwinkligen Dreiecken in einem Quader. Das ist die Lösungsidee zur Berechnung.☛


Bodendiagonale über Pythagoras


  • Lösungsidee:
  • Die Länge von jeweils zwei benachbarten Seiten muss bekannt sein.
  • Hat der Boden Rechteckform, sind diese Seiten immer rechtwinklig zueinander.
  • Die Bodendiagonale ist dann die Hypotenuse in einem 90°-Dreieck.

Bodendiagonale über Trigonometrie


  • Lösungsidee:
  • Die gesuchte Bodendiagonale ist die Hypotenuse.
  • Man muss die Länge einer der zwei kürzere Bodenseiten (Katheten) kennen.
  • Dann muss man noch einen Winkel dieser Seite mit der Hypotenuse kennen.