Basiswissen

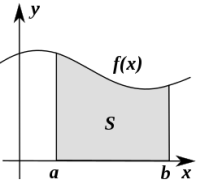
In der Wahrscheinlichkeitstheorie ist die Wahrscheinlichkeitsdichtefunktion, oft kurz Dichtefunktion, Wahrscheinlichkeitsdichte oder nur Dichte genannt, ein Hilfsmittel zur Beschreibung einer stetigen Wahrscheinlichkeitsverteilung. Die Integration der Wahrscheinlichkeitsdichte über ein Intervall [a, b] ergibt die Wahrscheinlichkeit dafür, dass eine Zufallsvariable mit dieser Dichte einen Wert zwischen a und b annimmt.

Bildbeschreibung und Urheberrecht — Jede x-Wert hat hier einen y-Wert zugeordnet. Der y ist die Wahrscheinlichkeitsdichte die zum x-Wert gehört. Die Wahrscheinlichkeit, dass das Ergebnis zwischen den Zahlen a und b liegt, ist gleich der Fläche unter der Kurve von a bis b. Berechnet wird diese Fläche oft über ein Integral. © AC (Wikimedia) ☛

Fußnoten

[1] Für die Physik erklärt ist das Wort in: David Halliday, Robert Resnick, Jearl Walker: Halliday Physik. Bachelor Edition. John Wiley & Sons. Inc. 2001. Deutsche Ausgabe. ISBN 978-3-527-40746-0. Seite 842 ff. Der Halliday ↗

[2] Eine weitere physikalische Deutung findet sich in: Richard Feynman: Feymnan-Vorlesungen über Physik. Band 3. Quantenmechanik. Oldenbourg Verlag. 2007. ISBN:978-3-486-58109-6. Seite 338.