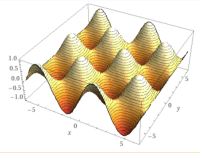
Mehrdimensionale Funktionen
f(x,y)
© 2016
- 2025
Basiswissen|
Hintergrundwissen|
Beispiele|
Das Semikolon als Trennzeichen|
Die unabhängigen Variablen als Tupel|
Fußnoten
Basiswissen
Definition: Die Dimension einer Funktion ist die Anzahl unabhängiger Variablen. Unabhängig nennt man die Variablen, für die man Zahlenwerte einsetzt. Das ist hier weiter erklärt.
Hintergrundwissen
Bei y=f(x) hat man nur die unabhängige Variable x. Diese Funktionsart ist also eindimensional [1]. Zweidimensional wäre z. B. z=f(x,y) [2]. Dreidimensional wäre z=f(w,x,y). Entsprechend spricht man von n-dimensionalen oder mehrdimensionalen Funktionen, wenn man mehr als eine unabhängige Variable hat. Siehe als Beispiel die 👉 zweidimensionale Funktion
Beispiele
- f(x;y) 👉 zweidimensionale Funktion
- f(w;x;y) 👉 dreidimensionale Funktion
- f(v;w;x;y) 👉 vierdimensionale Funktion
- f(R;fₚ;nₑ;fₗ;fᵢ;fₖ;L) 👉 siebendimensionale Funktion
Das Semikolon als Trennzeichen
Um die unabhängigen Variablen gegeneinander abzutrennen, findet man sowohl das Komm (,) wie auch das Semikolon (;) als Trennungszeichen. [2] Ein Grund, das Semikolon zu bevorzugen ist, dass man es auch noch nach dem Einsetzen von Funktionsargumenten, nämlich Zahlen weiterhin ohne Verlust der Eindeutigkeit als Trennungszeichen weiter verwenden kann.
f(x;y) -> mit x=2 und y=4,5 -> f(2;4,5)
Es ist in dem Beispiel offensichtlich, dass das Komma zu Mehrdeutigkeiten oder zumindest einer verwirrenden Art der Darstellung führen würde: f(2,4,5). Siehe mehr unter 👉 Trennzeichen
Die unabhängigen Variablen als Tupel
Wenn man bei einer mehrdimensionalen Funktion, zum Beispiel f(x)=x-y die Zahlen 4 und 7 eingibt, wird das Ergebnis ein anderes sein als bei der Eingabe von 7 und 4:
- f(4;7)=-3
- f(7;4)=+3
Wenn bei einer Menge von Dingen, etwa Zahlen, die Reihenfolge wichtig ist, spricht man in der Mathematik, speziell der Mengenlehre auch von einem 👉 Tupel
Fußnoten
- [1] Pampel T. (2010) Eindimensionale Funktionen. In: Mathematik für Wirtschaftswissenschaftler. Springer-Lehrbuch. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04490-8_5
- [2] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 3. 14. Auflage, 2019. ISBN: 978-3-658-11923-2. Verlag Springer Vieweg. Seite 404 bis 407 [am Beispiel zweidimensionaler Wahrscheinlichkeitssverteilung]
- [2] Zweidimensionale Funktionen sind ein Sonderfall von "Funktionen mehrerer unabhängiger Veränderlicher". Veränderliche heißt dabei so viel wie Variable. Als Beispiel dient die Abhängigkeit der Stromstärke I von der Spannung U und dem ohmschen Widerstand R. Als Funktion mehrerer unabhängiger Veränderlicher geschrieben als "I = f(U;R)". Das Trennungszeichen ist das Semikolon (;). In: Lehr- und Übungsbuch Mathematik. Band 1. Verlag Harri Deutsch. Thun und Frankfurt am Main. 20. Auflage. 1989. ISBN: 3-87444014. Dort das Kapitel "27 Funktionenen mehrerer unabhängiger Veränderlicher". Siehe auch 👉 zweidimensionale Funktion