Basiswissen

Das Kreuzprodukt, auch Vektorprodukt genannt, multipliziert zwei Vektoren so, dass als Ergebnis ein dritter Vektor entsteht. Als Multiplikationszeichen wird nur ein kleines Kreuz verwendet, daher der Name.

Bildbeschreibung und Urheberrecht — Das Rechenschema und die anschauliche Deutung des Kreuzproduktes von zwei Vektoren © Gunter Heim Acdx (Wikimedia) ☛

Wozu verwendet man das Kreuzprodukt?

Man kann zwei Vektoren so multiplizieren, dass wieder ein Vektor dabei herauskommt. Diesen Vektor nennt man das Kreuzprodukt. Dieser neue Vektor, das Ergebnis, steht immer senkrecht auf beiden Ausgangsvektoren.

Schreibweise

Korrekt: a×b

Falsch: a·b

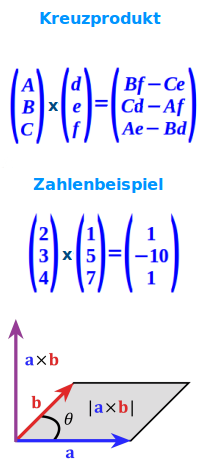
Das Kreuzprodukt berechnen

3D-Vektoren haben drei Koordinaten.

Der erste Vektor habe die Koordinaten (A;B;C).

Der zweite Vektor habe die Koordinaten (d;e;f).

Dann ist die oberste Koordinaten des Kreuzproduktes: Bf-Ce

Die mittlere Koordinate des Kreuzproduktes ist: Cd-Af

Die untere Koordinate des Kreuzproduktes ist: Ae-Bd

Siehe auch Kreuzprodukt berechnen ↗

Nicht Kommutativ

Die Kreuzmultiplikation ist nicht kommutativ.

a×b gibt etwas anderes als b×a.

Zwar bleibt die Länge des Ergebnisvektors gleich,

aber das Ergebnis zeigt in die entgegengesetzte Richtung.

Rechtssystem

Die zwei Ausgangsvektoren und ihr Kreuzprodukt sind ein Rechtssystem ↗

Das Kreuzprodukt als senkrechter Vektor

Das Kreuzprodukt c von zwei Vektoren a und b steht immer senkrecht auf diesen beiden Vektoren a und b.

Man sagt auch, der Ergebnisvektor ist orthogonal zu beiden Ausgangsvektoren. Siehe auch orthogonale Vektoren ↗

Das heißt: Das Kreuzprodukt c steht sowohl senkrecht auf dem Ausgangsvektor wie auch auf dem Ausgangsvektor b.

Das Kreuzprodukt als Normalenvektor

Stellt man sich die Vektoren a und b als Spannvektoren einer Ebene vor, dann ist das Kreuzprodukt von a und b für diese Ebene ein Normalenvektor. Siehe dazu auch Normalenvektor einer Ebene in Parameterform ↗

Das Kreuzprodukt als Parallelogrammfläche

Durch die zwei Ausgangsvektoren wird ein Parallelogramm aufgespannt.

Die Länge des Kreuzproduktes ist gleich dem Flächeninhalt des Parallelogramms.

Die Länge des Kreuzproduktes meint vom Kreuzprodukt den Vektorbetrag ↗

Siehe auch Parallelogrammfläche ↗

Gibt es ein Kreuzprodukt für 2D-Vektoren?

Nein: betrachtet man Vektoren in einem zweidimensionalen Raum, zum Beispiel in einem xy-Koordinatensystem, dann ist dafür das Kreuzprodukt nicht definiert^[1]. Das passt auch zu der Deutung des Vektorproduktes als ein Vektor, der senkrecht auf seinem beiden Ausgangsvektoren steht. Das ist für zwei nicht parallele Vektoren in einem xy-Koordinatensystem nicht möglich. Für zwei Vektoren, die nicht parallel zueinander sind und in einem xy-Koordinaten liegen, kann man keinen dritten Vektor finden, der senkrecht (orthogonal, 90°-Winkel) zu den beiden anderen Vektoren ist und ebenfalls ganz in dem xy-Koordinatensystem liegt. Eine eng verwandte Rechenart ist die Berechnung einer Determinante ↗

Der Sinus im Kreuzprodukt

Der Betrag des Kreuzproduktes ist gleich dem Produkt aus den Längen der Ausgangsvektoren und dem Sinus des eingeschlossenen Winkels. Siehe auch Sinus ↗

Synonyme

Kreuzprodukt ↗

Vektorprodukt ↗

Äußeres Produkt ↗

Fußnoten

[1] In dem Wikipedia-Artikel zum Kreuzprodukt wird dieses erst für Dimensionen größer 2 definiert: "Das Kreuzprodukt lässt sich für beliebige Dimension n ≥ 2 auf den den n-dimensionalen Raum verallgemeinern." In: Kreuzprodukt. Wikipedia. Abgerufen am 5. Dezember 2023. Online: https://de.wikipedia.org/wiki/Kreuzprodukt

[2] Auch das Spektrum Lexikon der Mathematik definiert das Kreuzprodukt nur für dreidimensionale Räume: "Vektorprodukt, äußeres Produkt, die Abbildung × : ℝ3 × ℝ3 → ℝ3, definiert durch […]" In: Guido Walz: Spektrum Lexikon der Mathematik. Band 5: Sed bis Zyl; 2002; ISBN: 3-8274-9437-1. Dort der Artikel: Kreuzprodukt. Online: https://www.spektrum.de/lexikon/mathematik/kreuzprodukt/5622