Heron-Verfahren
Wurzelziehen
© 2016
- 2025
Basiswissen|
Variante I: geometrisch|
Schritt 1: Startwerte|
Schritt 2: Durchschnitt als neues a|
Schritt 3: A durch a als neues b|
Schritt 4: zurück zu Schritt 2|
Die Wurzel von 20 als Zahlenbeispiel|
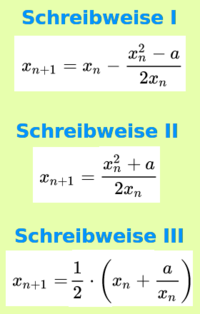
Variante II: rechnerisch|
Ein Zahlenbeispiel zu Variante II|
Was heißt Konvergenz?|
Was ist ein Algorithmus?|
Fußnoten
Basiswissen
Die Wurzel von 16 ist 4, denn 4·4 gibt 16. Aber was ist die Wurzel von der Zahl 6? Das Ergebnis ist eine sogenannte irrationale Zahl. Man kann sie also niemals exakt als Dezimalzahl angeben. Man kann sie aber mit beliebig vielen Nachkommastellen berechnen. Dazu dient das Heron-Verfahren. Es werden zwei Varianten vorgestellt.
Variante I: geometrisch
Die erste vorgestellte Variante ist nahe an der historischen Grundidee, die bis auf die alten Babylonier zurückgeht. Die Grundidee ist es, ein Quadrat zu finden, dessen Fläche der Zahl entspricht, für die man die Wurzel sucht. Die Seitenlänge des Quadrates ist dann die gesuchte Wurzel.[1]
Schritt 1: Startwerte
Wenn nun für die Zahl A (zum Beispiel 20) die Wurzel gesucht wird, dann denkt man sich zunächst irgendein beliebiges Rechtecke aus, das als Fächeninhalt genau A (hier also 20) hat. Ein solches Rechteck könnte zum Beispiel die Länge a=5 und die Breite b=2 haben. Wichtig ist, dass die Länge a auch wirklich für die längere der zwei Seiten steht.
Schritt 2: Durchschnitt als neues a
Als nächstes berechnet man den Durchschnitt, auch arithmetisches Mittel genannt[2] von der Länge und der Breite. Die Formel dafür ist (a+b):2. Man addiert also Länge und Breite. Das Ergebnis davon halbiert man dann, teilt es also rechnerisch durch zwei. Das Endergebnis ist der Durchschnitt. Im Beispiel: (2+10):2=6. Diesen Durchschnitt nimmt man jetzt als neuen Wert für die Länge des Rechtecks, also: a=6.
Schritt 3: A durch a als neues b
Als nächstes muss man die neue Breite b des Rechtecks bestimmen. Wenn man in Erinnerung behält, dass die Fläche ja immer den Wert von A haben soll (im Beispiel 20), und wenn weiterhin gilt, dass a·b=A geben muss, dann findet man b, wenn man A:a rechnet. Das kleine a ist jetzt das neue a aus dem vorherigen Schritt, also die 6. Man hat also: b=A:a. Im Zahlenbeispiel: b=20:6=10/3, also b gleich zehn Drittel. Man hat jetzt also: a=6 und b=10/3.
Schritt 4: zurück zu Schritt 2
Ab hier geht man mit den neuen Werten für a und b wieder zurück zu Schritt 2 und danach zu Schritt 3 und dann immer weiter so. Mit jedem Durchlauf dieser Schleife[3] rücken die Werte für a und b näher zusammen und auch näher an die gesuchte Wurzel heran.