Basiswissen

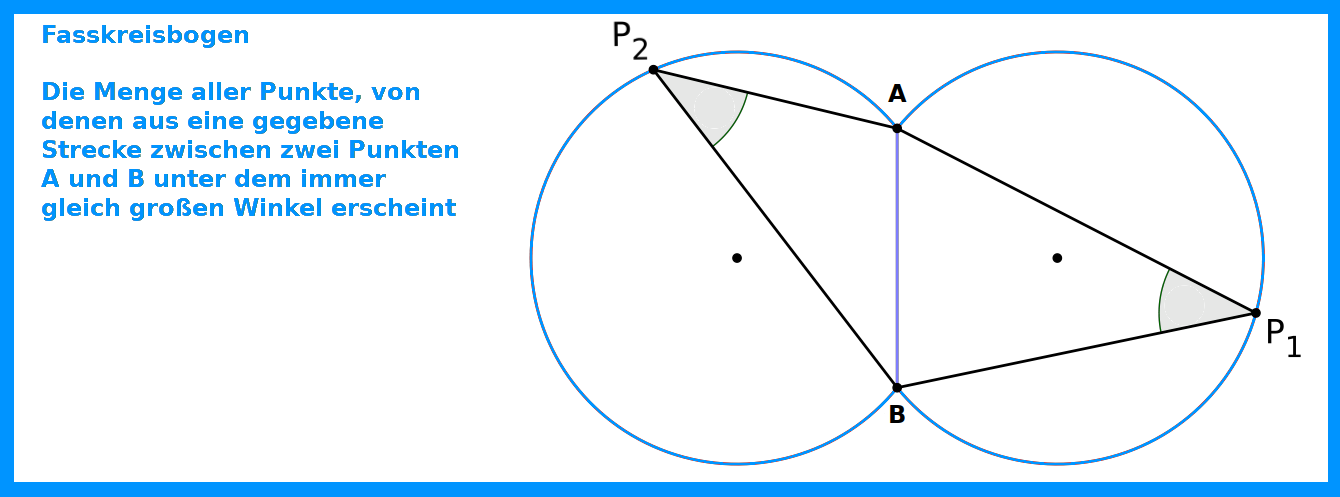
Als Fasskreisbogen über einer Strecke bezeichnet man Kreisbogen, von dem aus diese Strecke immer unter demselben Winkel erscheint. Der Thaleskreis ist ein Sonderfall des Fasskreisbogen, da der Winkel unter dem Punkt C auf dem halbkreis immer 90 Grad ist. Der Fasskreisbogen wird dazu verwendet, um Dreiecke mit einem speziellen Winkeln (verschieden von 90 Grad-Winkeln) zu konstruieren.

Bildbeschreibung und Urheberrecht — Ein Fasskreisbogen, besser eigentlich Fasskreisbogenpaar, entsteht, wenn man alle Punkte marktiert, von denen aus gesehen eine gegebene Strecke AB unter demselben, das heißt einem immer gleich großen Winkel, zu sehen ist. © Kmhkmh (Wikimedia) ☛

Kinästhetisches Lernen

Einen Fasskreisbogen laufen zu können ist ein schönes Beispiel für das sogenannte kinästhetische Lernen: man sucht sich zwei hohe und schlanke Objekte aus. Zwei Bäume die wenige Meter voneinander entfernt auf einem Spielplatz stehen sind ideal. Es können aber auch zwei Stangen oder sonst etwas sein. Wichtig ist, dass der Platz um die zwei Objekte frei und gut begehbar ist. Dann streckt man den rechten Arm ganz aus, spreizt Daumen und kleinen Finger zu einer große Spanne ab und kneift das linke Auge zu. Man muss nun die Spanne immer orthogonal (senkrecht) zum ausgestreckten Arm halten. Dann sucht man eine Position, von der aus je eines der Enden der abgespreizten Finger je eines der Objekte optisch überdeckt (sogenannte Deckpeilung). Jetzt versucht man andere, möglichst viele, Punkte im Gelände zu finden, von denen aus das der Fall ist. Findet man sehr viele solcher Punkte, kann man diese gedanklich oder durch Scharrmarken der Füße auf dem Boden zu einem Fasskreisbogen verbinden. Siehe mehr unter kinästhetisches Lernen ↗