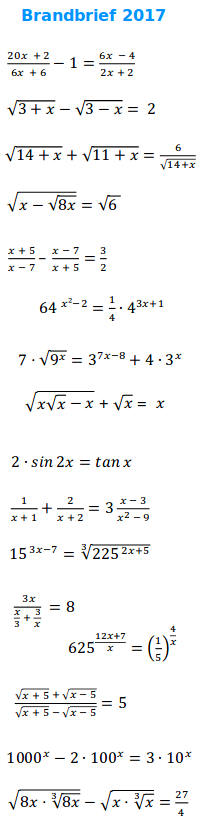Brandbrief 2017
Mathematik
© 2016
- 2025
Basiswissen|
Der Vorwurf|
Die Ursachen|
Die Lösung|
Beispiele|
Bewertung seitens einer Lernwerkstatt|
Kein Zahlenverständnis|
Es fehlen gut Bücher|
Zerstörte Freude|
Fußnoten
Basiswissen
Am 17. März 2017 veröffentlichten rund 130 Hochschulprofessoren und andere Fachpersonen einen öffentlichen Brandbrief[1] über den schlechten Zustand der mathematischen Vorbildung von Studenten. Der Adressat waren die Vorsitzende der Kultusministerkonferenz sowie andere Entscheidungsträger. Gegenstand des Schreibens waren vermeintlich abnehmende Mathematik-Fähigkeiten seitens der Studienanfänger.
Der Vorwurf
Die Unterzeichner beschrieben einen starken Rückgang der mathematischen Fähigkeiten von Studienanfängern in technischen und wirtschaftswissenschaftlichen Studiengängen. Studienanfängern "fehlen Mathematikkenntnisse aus dem Mittelstufenstoff, sogar schon Bruchrechnung(!), Potenz- und Wurzelrechnung, binomische Formeln, Logarithmen, Termumformungen, Elementargeometrie und Trigonometrie." Die Defizite seien auch in Vor- oder Brückenkursen nicht mehr aufholbar. Dies sei umso mehr eine Enttäuschung auch für die Studenten, da sie oft mit guten Mathenoten ein Studium aufgenommen hätten. Nachgewiesenermaßen entscheide gerade der Mittelstufenstoff über den Studienerfolg in den MINT-Fächern.
Die Ursachen
Die Ursache für die Defizite sehen die Autoren im Konzept der Kompetenzorientierung. In der Schule würde auf jeder Doppelseite im Buch ein neues Thema begonnen, alles ähnele einem kaleidoskopartigen Panorama ohne roten Faden. Alles werde nur häppchenweise und ohen Vernetzung angeboten.
Die Lösung
- Die Schulen sollen die Verantwortung für den Mittelstufenstoff übernehmen.
- Bruch- und Wurzelgleichungen, Elementargeometrie und Trigonometrie gehören zurück in den Lehrplan.
- Taschenrechner und CAS-Systeme sollen das Erlernen der Grundlagen nicht behindern.
- Symbolische-formale und abstrakte Inhalte sollen wieder stärker behandelt werden.
- Gekünstelte Modellierungsaufgaben sollen durch international anerkannte Aufgabentypen ersetzt werden.
- (Die Forderungen sind hier leicht verkürzt und umformuliert wiedergegeben.)
Beispiele
- Es folgen einige Aufgaben aus dem Brandbrief. Sie sollen in etwa das gewünschte Niveau wiedergeben, wie der Mittelstufenstoff zum Beginn des Studiums gekonnt werden sollte.
- Der Umfang eines Rechtecks beträgt 38 cm. Das Quadrat über der Diagonalen hat einen Flächeninhalt von 205 cm2. Berechnen Sie die Länge und Breite des Rechtecks! -
- Ein leeres Schwimmbecken kann durch eine Zuleitung in 20 Stunden gefüllt werden. Dasselbe Schwimmbecken kann durch den Abfluss in 28 Stunden vollständig entleert werden. Zu Beginn der Badesaison ist das Becken leer. Der Bademeister dreht die Zuleitung auf, vergisst aber, den Abfluss zu schließen. Wie viele Stunden dauert es, bis das Becken trotzdem voll ist?
- Um jeden Eckpunkt eines Quadrates wird ein Kreis gezeichnet, dessen Radius so groß ist wie die halbe Diagonale des Quadrates. Die vier Kreise haben mit den vier Quadratseiten insgesamt acht Schnittpunkte. Zeigen Sie, dass diese acht Punkte die Eckpunkte eines regelmäßigen Achtecks sind.
- Ein Quader mit einer Oberfläche von 8800 cm² hat eine Raumdiagonale der Länge 90 cm. Wie lang sind die 12 Kanten des Quaders zusammen?
- Ein Quader hat als Grundfläche ein Rechteck mit den Seiten a=26 und b=24. Wie muss die Höhe h des Quaders gewählt werden, wenn zwei Raumdiagonalen des Quaders senkrecht aufeinander stehen sollen? Berechnen Sie zwei mögliche Werte für h.
- Ein Quader hat Kanten der Länge 3 m, 4 m und 12 m. Von den vier Raumdiagonalen des Quaders werden zwei ausgewählt und ihr Schnittwinkel berechnet. Welche Ergebnisse sind dabei möglich?
- Ein Dreieck hat zwei gleich große Seiten der Länge l = 17cm und den Flächeninhalt A = 120 cm². Berechnen Sie zwei mögliche Werte für die Länge der dritten Seite!
- Gegeben ist ein Holzmodell in Form eines Kegels mit der Höhe h = 20݄ cm Der Kegel soll durch einen Schnitt parallel zur Grundfläche in zwei volumengleiche Teile zersägt werden. In welcher Höhe über der Grundfläche muss der Schnitt ausgeführt werden?
- Um wie viel Prozent ändert sich der Flächeninhalt eines rechtwinkligen Dreiecks, wenn man eine Kathete um 20 % verkürzt und die andere um 20 % verlängert? b) Eine Gurke besteht zu 90 % aus Wasser und wiegt 500 g. Nach einigen Tagen in der Küche ist ein Teil des Wassers verdunstet, und die Gurke besteht nur noch zu 80 % aus Wasser. Wie schwer ist sie dann?
Bewertung seitens einer Lernwerkstatt
Seit 2010 unterrichten wir die Fächer Mathematik, Physik und Chemie in der Mathe-AC Lernwerkstatt in Aachen. Wir stimmen dem Schreiben oben voll zu. Wir sehen die Dramatik eher sogar noch schärfer. Viele unserer Schüler sind hoch interessiert an der Mathematik, mindestens normal begabt und viele schreiben oft auch dauerhaft akzeptable bis gute Noten. Und dennoch sehen wir, wie auch für sie die oben beschriebenen Defizite zutreffen. Der Befund des Brandbriefes spiegelt sich in unserer Alltagspraxis wider:
Kein Zahlenverständnis
Ein Schüler im Abiturjahrgang kann mit Hilfe eines GTR problemlos berechnen, wie groß die Wahrscheinlichkeit ist, beim 10-maligen Werfen einer Münze genau 4 mal Kopf zu werfen. In der entsprechenden Arbeit schrieb er eine 2+. Derselbe Schüler konnte aber selbst nach längerem Überlegen nicht sagen, wie viele 6er man bei einem normalen Würfel bei 200 Würfen erwarten kann.
Eine Schülerin der Klasse 12 kann mit Hilfe eines GTR schnell und sicher eine Kurvendiskussion durchführen, auch für transzendente Funktionen. Ohne GTR gelingt es ihr auch nach längerem Überlegen nicht, den Funktionswert für x=0,25 der Funktion f(x)=1/x zu bestimmen.
Es fehlen gut Bücher
Was uns im täglichen Unterricht fehlt sind Zeit und Ruhe, die Grundlagen zu trainieren und zu wiederholen. Die Kinder klagen häufig darüber, dass ständig neue Sachen kämen und sie keinen Zusammenhang erkennen. Zudem fehlen solide Mathematikbücher. In den Büchern findet man kaum mehr kleinschrittige Erklärungen. Aus unserer Sicht ideal wäre ein Standardwerk, das die Schüler über alle Schuljahre hinweg begleitet (wie es etwa in Singapur der Fall ist). Siehe auch Mathematik Lehrbücher ↗
Zerstörte Freude
Besonders betonen möchten wir, dass so gut wie alle Schüler in den Klassen 1 bis 4 in hohem Maße an Mathematik und Sachwissen interessiert sind. In den Klassen 5 bis 9 erfolgt dann ein drastischer Einbruch. Am Ende wollen viele Physik so schnell wie möglich abwählen und Mathematik nur noch "weghaben". Der Grund ist nicht in den Kindern zu sehen. Es ist die Frustration über einen zerrissenen und überambitionierten Schulstoffe, die ihnen die Freude genommen hat. Wir hoffen, dass Brandbriefe wie der oben beschriebene eine möglichst große Wirkung haben.
Fußnoten
- [1] Brandbrief an die Kultusministerkonferenz und andere Institutionen. Unterzeichnet von 130 Professoren. 17. März 2017. Online: https://www.tagesspiegel.de/wissen/downloads/offener-brief-der-mathematiker
- [2] [G. Henn; C. Polaczek (2007) Studienerfolg in den Ingenieurwissenschaften. In: Das Hochschulwesen, 55. Jg./Heft 5, S. 144 -147.]