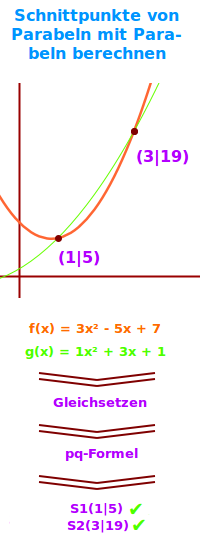Schnittpunkte von Parabeln mit Parabeln berechnen
10 Standardaufgaben für den Einstieg
Bei den Aufgaben a bis e gibt es vier mal zwei Schnittpunkte und einmal einen Schnittpunkt. Die Ergebnisse bestehen immer aus ganzen Zahlen (keine Kommazahlen). Das xx meint so viel wie x mal x, also x-quadrat.
a)
f(x) = 4xx + 4x + 22
h(x) = 2xx + 4x + 40
b)
f(x) = 4xx + 4x + 22
h(x) = 2xx + 4x + 72
c)
f(x) = 4xx + 4x - 50
h(x) = 1xx + 4x - 2
d)
f(x) = 4xx + 6x + 4
h(x) = 2xx + 2x + 10
e)
f(x) = 4xx + 20
h(x) = 3xx + 36
Bei den Aufgaben f bis j kommt vier mal ein Schnittpunkt und einmal zwei Schnittpunkte heraus. Das Dach ^ meint "Quadrat" oder "hoch zwei". Bei den Aufgaben mit Klammern unter dem Quadrat kann man normal gleichsetzen. Dann löst man am besten erst die Klammer auf und macht dann weiter wie normal.
f)
f(x) = 8xx + 4x + 4
h(x) = 4xx + 4x + 4
g)
f(x) = 4(x-2)^2 + 4
h(x) = 2(x-2)^2 + 4
h)
f(x) = (x+2)^2
g(x) = (x+4)^2
i)
f(x) = 4xx + 2x + 24
g(x) = 4(x-8)^2
j)
f(x) = 4xx - 8x + 8
g(x) = -4xx - 2x + 28
Lösungen
a) S1(3|70) und S2(-3|46)
b) S1(5|142) und S2(-5|102)
c) S1(4|30) und S2(-4|-2)
d) S1(1|14) und S2(-3|22)
e) S1(4|84)
f) S(0|4)
g) S(2|4)
h) S(-3|1)
i) S(4|64)
j) S(2|8)