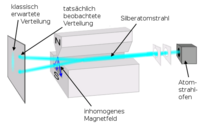
Stern-Gerlach-Versuch

Quantenphysik

Basiswissen｜ Beschreibung｜ Der Ofen und das Magnetfeld｜ Die Silberatome｜ Der Zufall｜ Klassische Vorhersage｜ Effekt bei einem Durchgang｜ Effekte bei mehreren Durchgängen｜ Sz und noch mal Sz｜ Sz dann Sx｜ Sz dann Sx dann Sz｜ Fußnoten

Basiswissen

Ein Strahl elektrisch neutraler Silberatome, die jedoch ein magnetisches Dipolmoment haben, wird durch ein inhomogenes Magnetfeld geschickt und spaltet sich dort in zwei Teilstrahlen auf. Damit wurde eine schon seit spätestens 1916 vermutete^[3] Richtungsquantelung^[5] experimentell bestätigt.

ZITAT:

"Dieses Experiment zeigt auf dramatische Weise die Notwendigkeit einer radikalen Abkehr von den Konzepten der klassischen Physik."^[6]

Beschreibung

Das Stern-Gerlach-Experiment ist in vielen Lehrbüchern der Physik beschrieben. Die Darstellung hier orientiert sich "am Sakurai"^[6] einem Lehrbuch das sich vor allem an Studierende richtet.

Der Ofen und das Magnetfeld

Zunächst werden Silberatome in einem Ofen stark erhitzt. Die Atome können den Ofen durch ein kleines Loch verlassen. Nach dem Verlassen werden sie durch einen sogenannten Kollimator zu einem möglichst engen Strahl gebündelt. Dann geht dieser Strahl durch ein inhomogenes Magnetfeld. Inhomogen heißt, dass das Magnetfeld an verschiedenen Orten auch eine unterschiedliche Stärke oder Richtung der Feldlinien hat.^[7] In einem homogenen Magnetfeld würde ein Magnet oder ein magnetischer Dipol^[10] bestenfalls kurz auf der Stelle gedreht werden. Eine Bewegung im Raum, eine sogenannte Translation, würde die Magnete aber nicht erfahren. Nur in einem inhomogenen Magnetfeld wird ein Magnet entlang einer Linie durch den Raum bewegt.

Die Silberatome

Die Silberatome haben 47 Elektronen in ihrer Elektronenhülle. In einem vereinfachten Modell bilden die 46 inneren Elektronen eine radialsymmetrische Elektronenwolke. Ihr resultierender Spin oder magnetisches Moment ist 0. Das äußere, ungepaarte Elektron, mit der Nummer 47, hat jedoch keine anderen Elektronen mit denen es seinen Spin ausgleichen könnte. Da die Elektronen fest mit dem Kern des Atoms verbunden sind, ist das magnetische Moment des äußersten Elektrons auch gleich dem magnetischen Moment des ganzen Atoms. (Der Spin des Kerns kann wegen seiner geringen Größe vernachlässigt werden.) Spin und magnetisches Moment sind zueinander proportional.^[8] Der Spin ist in der Physik eine sogenannte Vektorgröße. Die Vektoren für den Spin kann man sich anschaulich als Pfeil denken, der in eine bestimmte Richtung zeigt.

Der Zufall

Wenn die Atome den Ofen verlassen, so eine berechtigte Annahme, sind sie bezüglich der Richtung ihres Spins völlig zufällig ausgerichtet. Der Spin eines jeden einzelnen Atoms kann unabhängig von allen anderen Atomen in irgendeine zufällige Richtung im Raum zeigen. Es gibt auch keine bevorzugte Richtung, in die die Spins tendieren. Damit haben die Atome auch keine bevorzugte Richtung, in der das Magnetfeld stärker oder schwächer auf sie einwirken sollte.

Klassische Vorhersage

Der Nordpol des Magnetfeldes wird im Experiment als oben liegend und der Südpol als unten liegend betrachtet. Von unten nach oben zeigend denkt man sich die z-Achse eines Koordinatensystems. Wenn das magnetische Dipolmoment und damit auch der Spin größer als 0 sind, dann erfährt das Atom eine Kraft nach unten. Wenn das magnetische Dipolmoment und damit auch der Spin kleiner als 0 sind, dann erfährt das Atom eine Kraft nach oben:

Nordpol oben, Südpol unten

Von unten nach oben: z-Achse

Spin > 0, Kraft nach unten (↓)

Spin < 0, Kraft nach oben (↑)

Was sollte nun passieren, wenn die Atome vom Ofen kommend mit ihren völlig zufällig gerichteten Spins durch das Magnetfeld gehen? Wenn der Spin zufälligerweise orthogonal (senkrecht, 90°) zur Richtung der Magnetfeldlinien steht, ist die Kraft auf das Atom maximal. Steht der Spinvektor parallel oder antiparallel zu den Feldlinien, ist die Kraft Null.^[16] Für alle Winkel dazwischen gibt es ein kontinuierlichen Übergang von keiner Kraft (Null Kraft) zu maximaler Kraft. Das heißt: wenn die Atome mit Spins in zufälligen Richtungen aber ohne bevorzugte Raumrichtung insgesamt vom Ofen ins Magnetfeld eintreten, sollten sie nach klassisch-physikalischer Vorstellung vom Magnetfeld auch unterschiedlich weit von ihrer vorherigen geradlinigen Flugbahn abgelenkt werden. Nach der klassischen Physik sollte man erwarten, dass die Atome sehr viele verschiedene Auslenkungen in senkrechter Richtung erfahren. Fängt man die Silberatome auf einem Schirm auf, auf den sie nach dem Durchgang durch das Magnetfeld treffen, sollte man in vertikaler z-Richtung Atome in sehr vielen unterschiedlichen Entfernungen zu dem Punkt auf dem Schirm finden, auf den sie ohne Ablenkung getroffen wären. Man würde eine kontinuierliche Verteilung der Atome in senkrechter Richtung erwarten. Aber genau das tritt nicht ein.^[9]

Effekt bei einem Durchgang

Tatsächlich zeigt sich auf einem Schirm, den man in Flugrichtung der Atome kurz hinter dem Magnetfeld platziert ein enger Punkt von Silberatomen oben und ein enger Punkt von Silberatomen unten.^[9] Das ist nach der klassischen Physik, wie oben erläutert, sehr überraschend. Das Ergebnis, wenn der Strahl aus Silberatomen einmal durch das Magnetfeld geht, zeigt, dass der Spin bezüglich des Raumes relativ zu einer Richtung, beim Stern-Gerlach-Versuch oft die z-Richtung genannt, nur zwei feste Werte zu haben scheint. In der Frühzeit der Quantenphysik bezeichnete man diesen Befund als Richtungsquantelung.^[2]

Effekte bei mehreren Durchgängen

Man kann den Strahl aus Silberatomen auch zwei mal durch ein aufspaltendes Magnetfeld schicken. Nach dem Durchgang durch das erste inhomogene Magnetfeld geht ein Teil des vorher gespaltenen Strahls durch ein zweites inhomogenes Magnetfeld. Man spricht auch von einem sequentiellen Stern-Gerlach-Versuchen.^[12] Dabei werden oft zwei verschiedene Varianten betrachtet: zweimal eine Aufspaltung nach Sz und einmal erst Sz und dann Sx.

Sz und noch mal Sz

Nach dem Durchgang durch das erste Magnetfeld ist der Strahl in z-Richtung (oben-unten) in einen oberen und einen unteren Strahl aufgespalten. Nur wird nur der obere Strahl erneut durch ein Magnetfeld geschickt, das räumlich genauso ausgerichtet ist wie das erste, also den Strahl in oben und unten zerlegen würde. Tatsächlich kommen aus diesem zweiten Durchgang nur Silberatome mit einer Ablenkung nach oben heraus. Das ist genau das, was man auch "der gesunder Menschenverstand" erwarten würde:

Aus dem Ofen: alle Spin-Richtung zufällig verteilt

Vor dem ersten Durchgang: alle möglichen Richtungen

Das erste Magnetfeld trennt in z-Richtung (Sz⁺ und Sz⁻ als mögliche Ergebnisse)

Nach dem ersten Durchang, nach Sz: Ablenkung in Sz⁺ und Sz⁻ wird beobachtet.

Vor dem zweiten Durchgang: es werden nur Atome mit Sz⁺ genommen

Das zweite Magnetfeld trennt wieder in z-Richtung (Sz⁺ und Sz⁻ als mögliche Ergebnisse)

Nach dem zweiten Durchgang, nach Sz: Ablenkung nur nach Sz⁺ wird beobachtet.

Aus dem ersten Durchgang traten also Atome der Art Sz⁺ und Sz⁻ aus dem ersten Magnetfeld aus. Man hat dann nur den Strahl mit den Atomen Sz⁺ in ein zweites Magnetfeld geschickt. Erwartungsgemäß erschienen dann nach dem Durchgang durch das zweite Magnetfeld auch nur Atome mit der Eigenschaft Sz⁺. Die Atome mit der Eigenschaft Sz⁻ sind also, so könnte man denken, durch die doppelte Anordnung mit zwei Magnetfeldern erfolgreich aussortiert worden. Wir werden aber gleich sehen, dass diese Deutung nicht zutreffen kann.

Sz dann Sx

Nun wird der Strahl aus Silberatomen wieder durch zwei Magnetfelder geschickt. Aber diesmal trennt das erste Magnetfeld den Strahl wie vorher in z-Richtung, also in Sz⁺ und Sz⁻. Davon wird dann nur der Strahl mit Sz⁺ in das zweite Magnetfeld geschickt. Dieses zweite Magnetfeld trennt den Strahl in x-Richtung. Die x-Richtung wird dabei als waagrecht und rechtwinklig zur Flugbahn gedacht.

Aus dem Ofen: alle Spin-Richtung zufällig verteilt

Vor dem ersten Durchgang: alle möglichen Richtungen

Das Magnetfeld trennt in z-Richtung (Sz⁺ und Sz⁻ als Ergebnisse)

Nach dem ersten Durchang, nach Sz: Aufspaltung in Sz⁺ und Sz⁻

Vor dem zweiten Durchgang: es werden nur Atome mit Sz⁺ genommen

Das zweite Magnetfeld trennt diesmal in x-Richtung (Sx⁺ und Sx⁻ als mögliche Ergebnisse)

Nach dem zweiten Durchgang, nach Sx: Ablenkung nur nach Sx⁺ und Sx⁻ wird beobachtet, mit gleicher Stärke.

Bedeutet das, dass die Hälfte der Atome, die das erste Magnetfeld als Sz⁺ verließen zur Hälfte aus Sz⁺-Atomen bestanden, die gleichzeitig auch die Eigenschaft Sx⁺ hatten, während die andere Hälfte aus Sz⁺-Atomen die Eigenschaft Sx⁻ hatte? Diese Deutung wäre zum jetzigen Stand der Erkenntnisse möglich, erzeugt aber gleich beim dreistufigen Stern-Gerlach-Versuch große Probleme.

Sz dann Sx dann Sz

Nun wird der Strahl aus Silberatomen durch ein drittes Magnetfeld geschickt. Im ersten Schritt hat man nach der klassischen Vorstellung die Atome in die Eigenschaften Sz⁺ und Sz⁻ getrennt. Beim zweiten Durchgang hat man nur die Atome mit Sz⁺ in die Messaparatur (das Magnetfeld) hinein gelassen. Das heißt, dass alle Atome mit Sz⁻ aussortiert worden sind. Eigentlich.

Aus dem Ofen: alle Spin-Richtung zufällig verteilt

Vor dem ersten Durchgang: alle möglichen Richtungen

Das Magnetfeld trennt in z-Richtung (Sz⁺ und Sz⁻ als Ergebnisse)

Nach dem ersten Durchang, nach Sz: Aufspaltung in Sz⁺ und Sz⁻

Vor dem zweiten Durchgang: es werden nur Atome mit Sz⁺ genommen

Das zweite Magnetfeld trennt diesmal in x-Richtung (Sx⁺ und Sx⁻ als mögliche Ergebnisse)

Nach dem zweiten Durchgang, nach Sx: Ablenkung nur nach Sx⁺ und Sx⁻ wird beobachtet, mit gleicher Stärke.

Vor dem dritten Durchgang: es werden nur Atome mit Sx⁺ aus dem zweiten Durchgang genommen

Das dritte Magnetfeld trennt wieder in z-Richtung (Sz⁺ und Sz⁻ als theoretisch mögliche Ergebnisse)

Nach dem dritten Durchgang, nach Sz: Ablenkung sowohl in Sz⁺ als auch Sz⁻ wird beobachtet, mit gleicher Stärke.

Wiederum ist das Ergebnis im Sinne einer klassischen Physik völlig unverständlich. Wie können am Ende des dritten Durchganges Atome mit Sz⁻ erscheinen, wenn wir doch alle Atome mit Sz⁻ beim Eintritt in den zweiten Durchgang heraus gefilter hatten?^[14] Dass die Atome mit Sz⁻ eigentlich hätten herausgefilter sein müssen hatte ja der zweistufige Versuch der Art Sz -> Sz vorher gezeigt (siehe oben).

Fußnoten

[1] Stern, Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld, Z. f. Physik, Band 7, 1921, S. 249–253.

[2] Otto Stern, Walther Gerlach: Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. In: Zeitschrift für Physik. Band 9, 1922, S. 349–352. DOI: doi:10.1007/BF01326983

[3] P. Debye: Quantenhypothese und Zeemann-Effekt. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. Band 1916, 1916, S. 142–153 (eudml.org [abgerufen am 29. Oktober 2021]).

[4] Der Stern-Gerlach-Versuch mit Wasserstoffatomen: T. E. Phipps, J. B. Taylor: The Magnetic Moment of the Hydrogen Atom. Physical Review Band 29 (1927) S. 309–320

[5] Die Richtungsquantelung wird im englischen als "space quantiziation" bezeichnet. Der Ausdruck sei in der Frühzeit der Quantenmechanik üblich gewesen. In: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort auf Seite 11. Siehe auch Dirac-Notation ↗

[6] Die Übersetzung stammt von mir. Im englischen Original heißt es: "This experiment illustrates in a dramatic manner the necessity for a radical departure from the concepts of classical mechanics." Der Stern-Gerlach-Versuch ist neben dem Doppelspaltexperiment eines der zentralen Experimente zur Demonstration der Sonderbarkeiten der Quantenphysik. Diese Sonderbarkeiten, die enge Analogie zu ähnlichen Effekten im Zusammenhang mit der Polarisation von Licht sowie die formale Behandlung des Versuchs mit der Dirac-Notation mit Bras und Kets werden ausführlich behandelt in: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort auf Seite 11. Siehe auch Dirac-Notation ↗

[7] In einem homogenen Magnetfeld würde auf einen darin befindlichen Magneten keine resultierende Kraft wirken. Die Anziehung zum Nord- oder Südpol wären gleich groß, aber genau entgegengerichtet. Das klassische Beispiel für ein inhomogenes Magnetfeld ist das Magnetfeld eines Stabmagneten. Benachbarte Orte haben in der Regel auch (leicht) unterschiedliche Feldstärken und/oder Richtungen der Magnetfeldlinien. Siehe auch Magnetfeld ↗

[8] Das magnetische Moment wird auch bezeichnet als magnetisches Dipolmoment ↗

[9] "According to classical physics, the beam should have spread itself over a vertical distance corresponding to the (continuous) range of orientation of the magnetic moment. Instead, one observes [...], which is completely at odds with classical physics. The beam mysteriously splits itself into two parts, one corresponding to spin 'up' and the other to spin 'down'." Und: "Stern and Gerlach, however, observed the result in (b), namely that only two orientations of the magnetic moment manifested themselves. These two orientations did not span the entire expected range." In: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort auf Seite 4.

[10] Als magnetischen Dipol bezeichnet man entweder die mathematische Idealisierung eines Magneten oder aber auch mikroskopisch kleine Magnete in der Größenordnung von Elektronen, Atomen oder Molekülen. Beim Stern-Gerlach-Versuch besitzt jedes der 47 Elektronen im Silberatom ein magnetisches Moment (es verhält sich also wie ein winziger magnetischer Dipol). 46 dieser Elektronen heben sich in der Wirkung ihrer magnetischen Dipole paarweise gegenseitig auf. Für das gesamte Atom bleibt dann die Wirkung des 47ten Elektrons, jenes auf der äußersten Schale, übrig. Der magnetische Dipol des äußersten Elektrons macht dann sozusagen das ganze Silberatom zu einem magnetischen Dipol. Die Formel zur Berechnung der Kraft F eines magnetischen Dipolmoments μ⃗ in einem Magnetfeld B⃗ ist dann gegeben über die Formel F⃗ = ∇(μ⃗ · B⃗ ). Das umgedreht Dreieck ∇ ist der sogenannte Nabla-Operator. Geht es nur um die Stärke der Kraft, nicht aber die Richtung, kann man die Formel auch näherungsweise schreiben als |F| = |μ|·|∇B|·cos(θ). In dieser Schreibweise erkennt man, dass der Winkel θ zwischen der Richtung des magnetischen Dipolmoments (z. B. des Elektrons) und der lokalen Richtung der Magnetfeldlinien eine Rolle spielt. Das ist wichtig für den Stern-Gerlach-Versuch. Siehe auch magnetischer Dipol ↗

[11] Nathan Rosen and C. Zener: Double Stern-Gerlach Experiment and Related Collision Phenomena. Phys. Rev. 40, 502 – Published 15 May, 1932. Online: https://doi.org/10.1103/PhysRev.40.502

[12] Siehe das Kapitel "Sequential Stern-Gerlach Experiments" Dort sind die verschiedenen Varianten ausführlich und zsuammen mit der Dirac-Notation der Quantenphysik erklärt. In: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort ab Seite 4.

[13] Zur Deutung des zweistufigen Versuchs mit Sz und Sx: "Does it mean that 50% of the atoms in the Sz+ beam coming out of the first apparatus (SGz) are made up of atoms characterized by both Sz+ and Sx+, while the remaining 50% have both Sz+ and Sx-? It turns out that such a picture runs into difficulty". In: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort auf Seite 5.

[14] Das Ergebnis des dreistufigen Versuchs Sz -> Sx -> Sz ist völlig unerwartet: "It is observed experimentally that two components emerge from the third apparatus, not one; the emerging beams are seen to have both an Sz + component and an Sz- component. This is a complete surprise because after the atoms emerged from the first apparatus, we made sure that the Sz- component was completely blocked." In: J. J. Sakurai: Modern Quantum Mechanics. Addison-Wesley Publishing Company. 1985. ISBN: 0-8053-7501-5. Dort auf Seite 5.

[15] Die Silberatome, deren Spin (oder ihr magnetisches Moment) parallel zu den Feldlinien des Magnetfeldes dürften nach klassischer Deutung gar keine Ablenkung durch das Magnetfeld erfahren. Je mehr der Spin parallel zu den Linien des Magnetfeldes ist, desto weniger würde es abgelenkt: "We represent these particles' magnetic dipole fields by a vector p⃗ that points directly from south to north. As it is aligned along the axis of the particle's spin, p⃗ represents a direction or orientation for the particle. The Spin angular momentum vector S⃗ in other words, is proportional to p⃗: p⃗ ∝ S⃗." Und dann: "You might expect a third scenario, where the silver atom's magnetic field p⃗ was pointing sideways - orthogonal to either of the previous choices - perhaps parallel with the beam line. Classical electrodynamics predicts that such an atom would be undeflected, and continue on hit the screen as if the big magnet weren't even present. By extension, then, all possible intermediate cases would fill in all other possibilities, so that the beam would have been smeared out into a line. In other words, from this perspective, the silver atoms would form a vertical line on the screen." In: The Stern-Gerlach Experiment. ©2021 The Pasayten Institute. Winthrop, Washington (USA). Lizenziert nach cc by-sa-4.0. Online: https://pasayten.org/quantum-mechanics-for-working-professionals-old/the-stern-gerlach-experiment