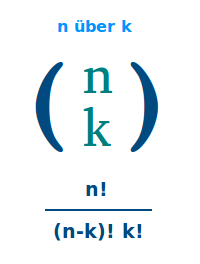n über k
n!/[(n-k)!k!]
Basiswissen
5 über 3 gibt ausgerechnet 10: man nennt den ganzen Ausdruck den Binomialkoeffizienten. Wichtig ist er in der Stochastik und Kombinatorik und steht im Zusammenhang mit dem Pascalschen Dreieck. Hier ist die Berechnung kurz erklärt.
Definition
- n über k = n! / [(n-k)!·k!]
Legende
- n = irgendeine natürliche Zahl ↗
- ! = das Fakultätszeichen ↗
- / = das Divisionszeichen ↗
Rechenbeispiel
- 5 über 3
- 5 über 3 = 5!/[(5-3)!·3!]
- 5 über 3 = 120/[2!·3!]
- 5 über 3 = 120/[2·6]
- 5 über 3 = 10
- 5 über 5 = 1
- 3 über 5 = 0
- 0 über 0 = 1
Sonderfall: n ist gleich k
- Ist k = n, ist das Ergebnis immer 1.
- Beispiel: 4 über 4 gibt genau 1.
- Auch 0 über 0 gibt per Definition genau 1.
- Siehe als Beispiel 1 über 1 ↗
Sonderfall: k ist genau 0
- Ist k = 0 ist das Ergebnis per Definition immer 1.
- Beispiel: 4 über 0 ist 1. Siehe auch n über 0 ↗
Sonderfall: n ist kleiner als k
- Ist n < k oder k > n ist das Ergebnis per Definition immer 0.
- Beispiel: 2 über 4 gibt genau 0.
Anwendung: Bernoulli-Ketten
- Der Binomialkoeffizient spielt im Thema Bernoulli-Ketten und Binomialverteilung eine Rolle.
- Er taucht dort in der Formel auf: B(n,k,p) = (n über k)·pᵏ·(1-p)ⁿ⁻ᵏ
- Mehr dazu unter Bernoulli-Ketten-Formel ↗
