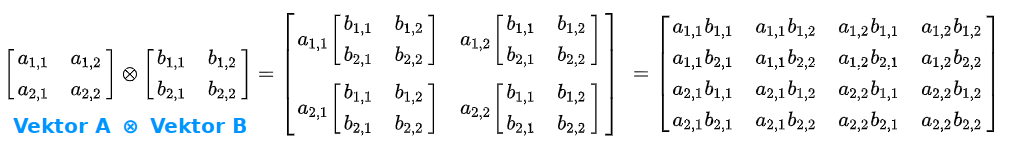Definition

Wenn A eine m×n‑Matrix ist und B eine p×q‑Matrix, dann ist A ⊗ B eine (m·p) × (n·q)‑Matrix, die entsteht, indem man jedes Element aᵢⱼ von A mit der gesamten Matrix B multipliziert.^[1] Das Kronecker-Produkt spielt unter anderem eine Rolle in der Quantenmechanik, insbesondere in der Bra-Ket-Notation nach Dirac. Es wird verwendet, um das Tensorprodukt von Zuständen und Operatoren darzustellen, was essenziell ist, um zusammengesetzte Quantensysteme und Verschränkung zu beschreiben. Zum Beispiel, wenn man zwei Quantensysteme mit den Zuständen ∣ψ₁⟩ und ∣ψ₂⟩ hat, dann ist der Zustand des zusammengesetzten Systems durch das Kronecker-Produkt ∣ψ₁⟩ ⊗ ∣ψ₂⟩ gegeben. Siehe auch Dirac-Notation ↗

Bildbeschreibung und Urheberrecht — Die Rechenregel zum Kronecker-Produkt: das Ergebnis hat in der Regel mehr Zeilen und mehr Spalten als jede der beiden Anfangsmatrizen.☛

Fußnoten

^[1] Hat man eine Matrix A mit m Zeilen und n Spalten und eine Matrix B mit p Zeilen und r Spalten, so entsteht daraus "eine neue Matrix vom Typ (m·p,n·r), die aus A dadurch entsteht, dass jedes Element von A mit der Matrix B multipliziert wird." In: