Definitionsbereich
Definition
Basiswissen
Alle Zahlen, zu denen es einen sinnvoll zuordenbaren y-Wert geben soll: das Wort Definitionsbereich wird zum Beispiel im Zusammenhang mit mathematischen Funktion, Aussagen oder Gesetzen gebraucht. Der Definitionsbereich sind alle x-Werte denen die Funktion eindeutig einen mathematisch oder sonstwie sinnvoll deutbaren y-Wert zuordnet.
Ein einführendes, praktisches Beispiel
Angenommen man hat eine Leiter der Länge 14 Meter. Diese soll auf einem waagrechten Untergrund in verschiedenen Abständen x zu einer senkrecht aufragenden Hauswand aufgestellt und an die Hauswand angelehnt werden. Das obere Ende der Leiter berührt die Hauswand dann in einer Höhe, die hier y genannt werden soll. Man kann dann jedem Wert für x genau einen Wert für y zuordnen.
Die erlaubten x-Zahlen auf dem Boden geben einen sinnvollen Definitionsbereich. Die sich dann daraus einstellenden Anlehnhöhen y der Leiter geben den dazu passenden Wertebereich.
Wenn x also den Abstand des Fußpunktes vom Haus meint, dann gibt es zwei Arten von x-Werten, für die es nicht sinnvoll ist, nach der Anstellhöhe y zu fragen: erstens, wenn die x-Werte genauso groß oder größer sind als die Leiter lang ist. Wenn die Leiter weiter weg vom Haus steht als sie an Länge hat, dann liegt sie einfach nur flach auf dem Boden. Und zweitens machen auch negative Werte für x keinen Sinn. Sie könnten vielleicht als Entfernung zur Wand im Hausinneren gedacht werden, aber in den meisten praktischen Fällen träfe das nicht zu.
- D = {x| 0 ≤ x ≤ 14}
Diese Schreibweise sagt: der Definitionsbereich ist die Menge aller Zahlen, die gleich groß oder größer sind als 0 und gleich groß oder kleiner als die 14 sind. Diese Zahlen sollen x genannt werden. Die Funktionsgleichung, die jedem x das dazugehörige y zuordnet ist y = √(196-x²). Und tatsächlich würde diese Funktionsgleichung für x-Werte größer als 14 negative Radikanden[4] ergeben, was mathematisch nicht definitiert ist.
Der Definitionsbereich von Funktionen
Bei einer mathematischen Funktion bezieht sich der Definitionsbereich immer auf die x-Werte. Der Definitionsbereich ist höchstens so groß wie die Menge aller x-Werte, denen eindeutig genau ein y-Wert zugeordnet ist. Man schreibt für den Definitionsbereich dann meist ein großes lateinisches D:
- f(x) = √x mit D = {0,R⁺}
- f(x) = 1/x mit D = R0
Im ersten Beispiel mit dem Funktionsterm √x ist der Definitionsbereich beschränkt auf die Zahl 0 und dann noch alle positiven reellen Zahlen[1]. Das heißt umgekehrt, dass man für x keine negativen Zahlen einsetzen kann, da diese nicht zum Definitionsbereich gehören[2].
- Beispiel: f(x)= √x mit D = {0,R⁺}
- Das heißt: man kann für x alle positiven reellen Zahlen einsetzen[1].
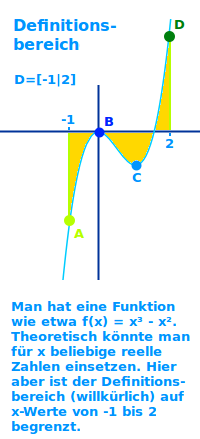
- Man darf für x Werte von -1 bis 2 einsetzen.
Der Definitionsbereich für Graphen
Eine Funktion hat nur innerhalb des Definitionsbereiches einen Graphen. Ist zum Beispiel f(x) = x² nur definiert für x-Werte zwischen 1 bis 3, dann wird auch der Graph nur von x=1 bis x=3 gezeichnet. Siehe auch Graph aus Funktionsgleichung ↗
Lücken im Definitionsbereich
Wenn der Definitionsbereich lückenlos alle Zahlen zwischen einer kleinsten und einer größten Zahl meint, dann spricht man auch von einem Definitionsintervall[3]. Hat ein Intervall allerdings Lücken, wo die Funktion nicht definiert ist, so spricht man entsprechend von einer Definitionslücke[4]. Die Funktion f(x)=1/(x-4) hat bei x=4 eine Definitionslücke. Denn würde man für x die Zahl einzetzen, müsste man eins geteilt durch 0 rechnen, was wiederum mathematisch nicht definiert ist. Eine typische Schreibweise ist D = R{4}. Das heißt: die Definitionsmenge ist die Menge aller reellen Zahlen aber ohne die Menge, die hier nur aus der Zahl 4 besteht. Siehe auch Definitionslücke ↗
Schreibweisen von Definitionsbereichen
- Als Abkürzung verwendet werden das D und das D mit doppelten Strich:
- D = [-1|2] = -1 und 2 gehören dazu beidseitig geschlossenes Intervall ↗
- D = ]-1|2[ = die -1 gehört nicht dazu beidseitig offenes Intervall ↗
- D = ]-1|2] = die -1 gehört nicht dazu linksoffenes Intervall ↗
- D = ]-1|2] = die 2 gehört dazu rechtsoffenes Intervall ↗
- D = [-1|2[ = die 2 gehört nicht dazu rechtsoffenes Intervall ↗
- D = N meint alle natürliche Zahlen ↗
- D = R meint alle reelle Zahlen ↗
- D = R {} meint alle rellen Zahlen ohne die 0
- D = {3; 7; -5; 20} meint die aufgelisteten Zahlen
- D = {x | x<5} meint: x derart dass x kleiner ist als 5
- D = {x | 2
- Mehr unter Mengenschreibweisen ↗
Der Definitionsbereich für eine mathematische Aussage
Die Aussage "malrechnen macht das Ergebnis nie kleiner als die kleinste der zwei Anfangszahlen war" gilt, solange man nur mit natürlichen Zahlen rechnet. Die natürlichen Zahlen beginnen bei der 1 und gehen dann in Einerschritten aufwärts. Solange man sich an diesen Definitionsbereich hält, etwa im Grundschulrechnen, ist die Aussage wahr. Möchte man die Aussage noch kürzer machen, kann man den Definitionsbereich auf natürliche Zahlen größer als 1 begrenzen und dann sagen: "malrechnen macht das Ergebnis immer größer als die kleinste der zwei Anfangszahlen war".
Der Definitionsbereich für eine nicht mathematische Aussage
Als Definitionsbereich oder auch Geltungsbereich bezeichnet man bei allgemein gehaltenen Aussagen, auf welche Gegenstände sie angewendet werden können. So kann man zum Beispiel im Wahlrecht definieren, dass alle Bürger ab 18 Jahren Lebensalter das aktive Wahlrecht haben sollen. Man muss dann weiter den Bereich der Personen definieren, die man als Bürger auffassen möchte. Soll das jede in einem Land geborene Person sein (etwa in den USA) oder muss man dazu einen dauerhaften Wohnsitz in dem Land haben oder einen gültigen Pass des Landes besitzen? Oder sollen erst Personen ab einem Mindestmaß an Besitz oder Einkommen als Bürger gelten (altes preußisches Wahlrecht)? Die Menschen, die zu den Bürgern zählen sollen, sind dann der Definitionsbereich der Aussage.
Synonyme für Definitionsbereich
Fußnoten
- [1] Ein R mit dem senkrechten Strich links oft doppelt geschrieben steht für alle reellen Zahlen. Reell ist jede Zahl, die irgendwo als Punkt auf einer Zahlengeraden gedacht werden kann. R⁺ steht dann für alle positiven Zahlen. Die Schreibweise {0,R⁺} bedeutet, dass zum Definitionsbereich, auch Definitionsmenge genannt sowohl die 0 wie auch alle positiven reellen Zahlen. Die 0 muss ausdrücklich mit genannt werden, da sie nicht als positive (und auch nicht als negative) Zahl gilt. Der mathematische Definitionsbereich ist oft (nicht immer) ein sogenanntes Intervall. Wie man Intervalle und auch andere Mengen schreibt steht im Artikel zu Mengenschreibweisen ↗
- [2] Welche Rolle negative Zahlen für die Wurzel spielen ist erklärt im Artikel zur Wurzelfunktion ↗
- [3] Als Intervall bezeichnet man einen zusammenhängenden Bereich ohne Lücken. Siehe mehr unter Intervall ↗
- [4] Als Radikand bezeichnet man den gesamten Term unter dem Wurzelzeichen, also das, woraus die Wurzel gezogen werden soll. Siehe mehr unter Radikand ↗
