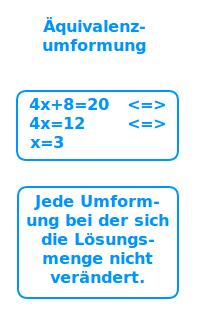
Äquivalenzumformung
⇔
© 2016
- 2025
Definition|
Wie lautet die Definition?|
Was meint "Lösungsmenge"?|
Was wäre eine Äquivalenzumformung?|
Was wäre keine Äquivalenzumformung?|
Wie schreibt man das?|
Aufgaben
Definition
Man formt eine Gleichung so um, dass sich ihre Lösungsmenge dabei nicht verändern kann. Das wird hier erklärt am Beispiel: 2·(x-4) = 12.
Wie lautet die Definition?
- Das Wort spielt beim Lösen von Gleichungen eine wichtige Rolle.
- Mit Äquivalenzumformungen kann man Schritt für Schritt schwere in leichte Gleichungen umformen.
- Eine Äquivalenzumformung ist eine Umformung, bei der sich die Lösungsmenge einer Gleichung nicht ändern kann.
Was meint "Lösungsmenge"?
- Nehmen wir die Gleichung 2·(x-4) = 12
- Wenn man für die Unbekannte x die Zahl 10 einsetzt, dann geht die Gleichung auf.
- Jede Zahl, die das "kann", würde man eine Lösung dieser Gleichung nennen.
- Bei der Gleichung oben ist die Zahl 10 die einzige Lösung.
- Also ist die Zahl 10 auch die ganze Lösungsmenge.
Was wäre eine Äquivalenzumformung?
- 2(x-4)=12 kann man noch durch Probieren lösen.
- Man könnte es aber auch über Umformungen lösen.
- Man könnte zum Beispiel erst beide Seiten der Gleichung durch 2 teilen.
- Das gäbe: x-4=6. Das ist jetzt eigentlich eine neue Gleichung.
- Aber auch bei ihr ist die einzige passende Lösung die Zahl 10.
- Das Teilen durch 2 war also eine Äquivalenzumformung.
- Jetzt kann man auf beiden Seiten die Zahl 4 addieren.
- Das gibt die neue Gleichung x=10.
- Auch hier ist die Lösungsmenge nur die Zahl 10.
- Auch die Addition war also eine Äquivalenzumformung.
Was wäre keine Äquivalenzumformung?
- Nehmen wir wieder: 2·(x-4)=12
- Man könnte beide Seiten der Gleichung mit 0 malnehmen.
- Dann gäbe das 0=0.
- So eine Gleichung nennt man eine "Identität".
- Egal was man für x "einsetzt", die Gleichung geht immer auf.
- Man sagt, dass die Lösungsmenge aus allen möglichen Zahlen besteht.
- Vor dem Malnehmen war die Lösungsmenge also 10, hinterher waren es alle Zahlen.
- Das Malnehmen mit 0 hat also die Lösungsmenge verändert.
- Beide Seiten einer Gleichung mit 0 malnehmen ist keine Äquivalenzumformung.
Wie schreibt man das?
- Normalerweise benutzt man den Äquivalenzpfeil ⇔ ↗
- In der Schulmathematik kommt auch der Umformungsstrich vor: |
Aufgaben
- In den Quickcheck-Aufgaben (qck) werden verschiedene Umformungen vorgenommen.
- Bei vielen ändert sich dabei die Lösungmenge.
- Es wird trainiert, das zu erkennen.
- Aufgaben unter => qck