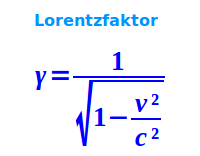
Lorentzfaktor
Physik
Basiswissen
Umrechnungsfaktor Gamma in der Relativitätstheorie: der dimensionslose Lorentzfaktor Gamma beschreibt in der speziellen Relativitätstheorie die Zeitdilatation sowie den Kehrwert der Längenkontraktion bei der Koordinatentransformation zwischen relativ zueinander bewegten Inertialsystemen.
Formel zum Lorentzfaktor
- γ = 1 / Wurzel aus [ 1 - (v²)/(c²)]
Legende
- γ = Lorentzfaktor, griechisches Gamma ↗
- v = Relativgeschwindigkeit zweier Bezugssysteme.
- c = Die Vakuum Lichtgeschwindigkeit ↗
Fakten zum Lorentzfaktor
- Die Werte für γ liegen zwischen 1 und unendlich ↗
- Die Funktion ist streng monoton steigend ↗
- Die Funktion ist nach oben unbeschränkt ↗
- Er ist proportional zur Zeitdilatation ↗
- Der Kehrwert ist proportional zur Längenkontraktion ↗